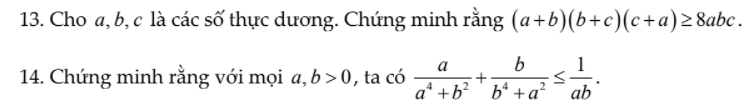Bài 1:
a) Ta có: \(A=\left(\dfrac{6+\sqrt{20}}{3+\sqrt{5}}+\dfrac{\sqrt{14}-\sqrt{2}}{\sqrt{7}-1}\right):\left(2+\sqrt{2}\right)\)
\(=\left(2+\sqrt{2}\right)\cdot\dfrac{1}{2+\sqrt{2}}\)
=1
b) Ta có: \(B=\sqrt{5-2\sqrt{6}}+\sqrt{5+2\sqrt{6}}-\dfrac{11}{2\sqrt{3}+1}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}-2\sqrt{3}+1\)
=1
Bài 2:
b) Ta có: \(\sqrt{9x^2-9}+\sqrt{4x^2-4}=\sqrt{16x^2-16}+2\)
\(\Leftrightarrow3\sqrt{x^2-1}+2\sqrt{x^2-1}-4\sqrt{x^2-1}=2\)
\(\Leftrightarrow x^2-1=4\)
\(\Leftrightarrow x\in\left\{\sqrt{5};-\sqrt{5}\right\}\)