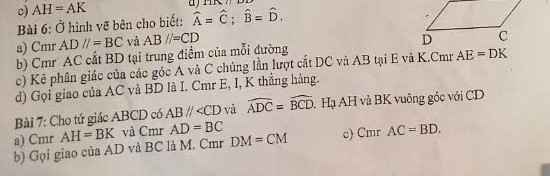Bài 6:
a: Ta có: \(\widehat{A}=\widehat{C}\)
\(\widehat{B}=\widehat{D}\)
Do đó: \(\widehat{A}+\widehat{D}=\widehat{B}+\widehat{C}\)
mà \(\widehat{A}+\widehat{D}+\widehat{B}+\widehat{C}=360^0\)
nên \(\widehat{A}+\widehat{D}=\dfrac{360^0}{2}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD
Ta có: \(\widehat{A}+\widehat{D}=180^0\)
mà \(\widehat{D}=\widehat{B}\)(GT)
nên \(\widehat{A}+\widehat{B}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AD//BC
Xét ΔABC và ΔCDA có
\(\widehat{BAC}=\widehat{DCA}\)(hai góc so le trong, AB//CD)
AC chung
\(\widehat{BCA}=\widehat{DAC}\)(hai góc so le trong, AD//BC)
Do đó: ΔABC=ΔCDA
=>AB=CD; BC=DA
b: Gọi giao điểm của AC và BD là O
Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
AB=CD
\(\widehat{OBA}=\widehat{ODC}\)(hai góc so le trong, AB//CD)
Do đó: ΔOAB=ΔOCD
=>OA=OC
=>O là trung điểm của AC
ΔOAB=ΔOCD
=>OB=OD
=>O là trung điểm của BD
c: Ta có: \(\widehat{DAE}=\dfrac{\widehat{DAB}}{2}\)(AE là phân giác của góc DAB)
\(\widehat{BCK}=\dfrac{\widehat{BCD}}{2}\)(CK là phân giác của góc BCD)
mà \(\widehat{DAB}=\widehat{BCD}\)
nên \(\widehat{DAE}=\widehat{BCK}\)
Xét ΔDAE và ΔBCK có
\(\widehat{DAE}=\widehat{BCK}\)
DA=BC
\(\widehat{ADE}=\widehat{CBK}\)
Do đó: ΔDAE=ΔBCK
=>AE=CK
d: I là giao điểm của AC và BD
=>I là trung điểm chung của AC và BD
Ta có: AK+KB=AB
CE+ED=CD
mà AB=CD và BK=DE
nên AK=CE
Xét ΔIAK và ΔICE có
IA=IC
\(\widehat{IAK}=\widehat{ICE}\)(hai góc so le trong, AK//CE)
AK=CE
Do đó: ΔIAK=ΔICE
=>\(\widehat{AIK}=\widehat{CIE}\)
=>\(\widehat{AIK}+\widehat{AIE}=180^0\)
=>K,I,E thẳng hàng
Bài 7:
a: Ta có: AH\(\perp\)CD
BK\(\perp\)CD
Do đó:AH//BK
Xét tứ giác ABKH có
AB//KH
AH//BK
Do đó: ABKH là hình bình hành
=>AH=BK
Ta có: \(\widehat{HAD}+\widehat{HDA}=90^0\)(ΔHAD vuông tại H)
\(\widehat{KBC}+\widehat{KCB}=90^0\)(ΔKBC vuông tại K)
mà \(\widehat{HDA}=\widehat{KCB}\)
nên \(\widehat{HAD}=\widehat{KBC}\)
Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AH=BK
\(\widehat{HAD}=\widehat{KBC}\)
Do đó: ΔAHD=ΔBKC
=>AD=BC
b: Xét ΔMDC có \(\widehat{MDC}=\widehat{MCD}\)
nên ΔMDC cân tại M
=>MC=MD
c: Xét ΔADC và ΔBCD có
AD=BC
\(\widehat{ADC}=\widehat{BCD}\)
DC chung
Do đó: ΔADC=ΔBCD
=>AC=BD