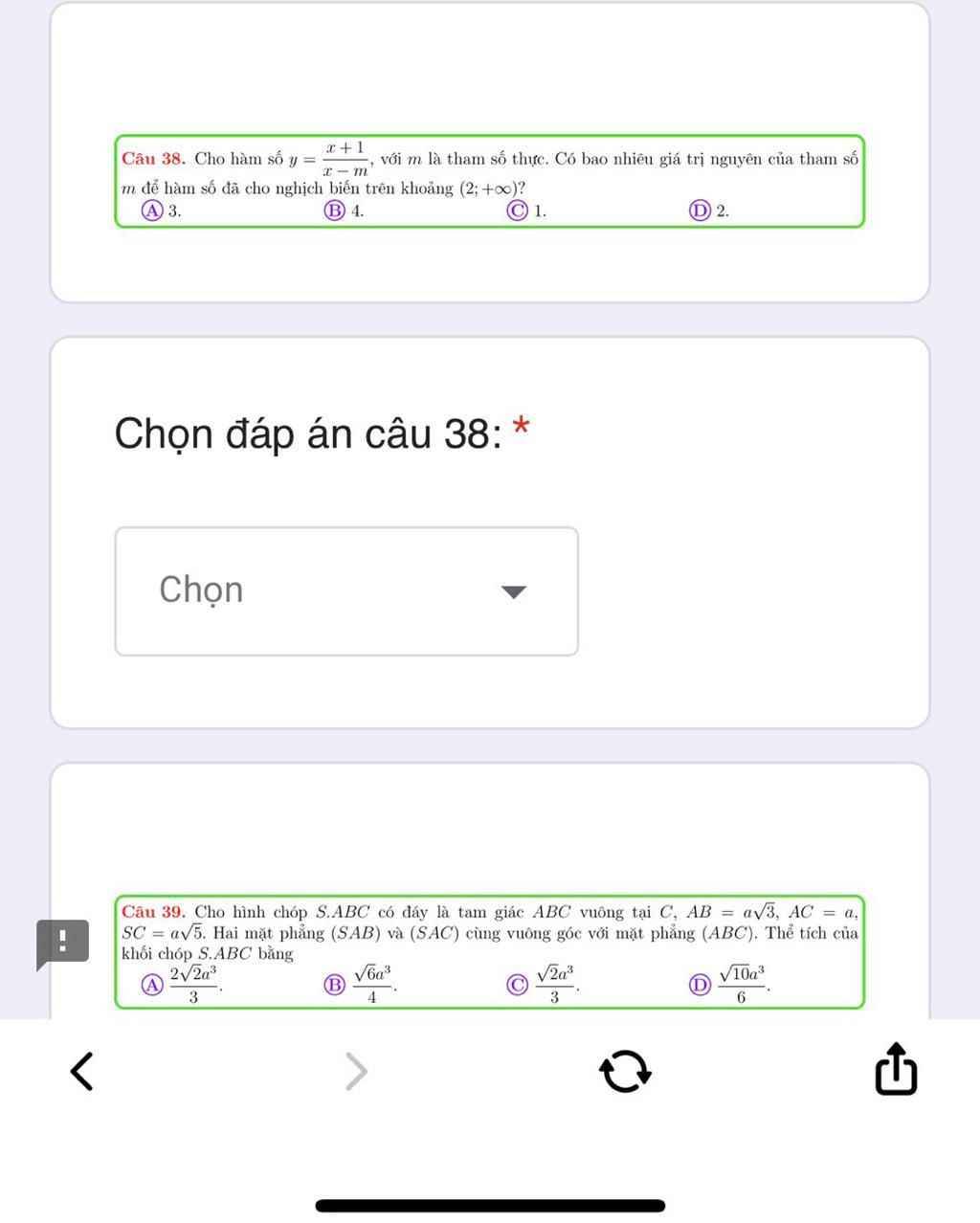
Câu 38: ĐKXĐ: `x-m#0; <=> m # x`
Mà `x ∈ (2; +∞); => m ∈ (-∞; 2]` hay `m ≤ 2` `(1)`
Ta có: `y^' = (-m-1)/(x-m)^2`
Để hàm số nghịch biến; `=> -m-1 < 0; <=> m > -1` `(2)`
Kết hợp `(1)` và `(2)` `=> -1 < m ≤ 2`
`=>` Giá trị nguyên của `m` là: `0; 1; 2`
`=>` Có `3` giá trị nguyên
`=>` Chọn `A`
---------------------------------------------------------------------------------------
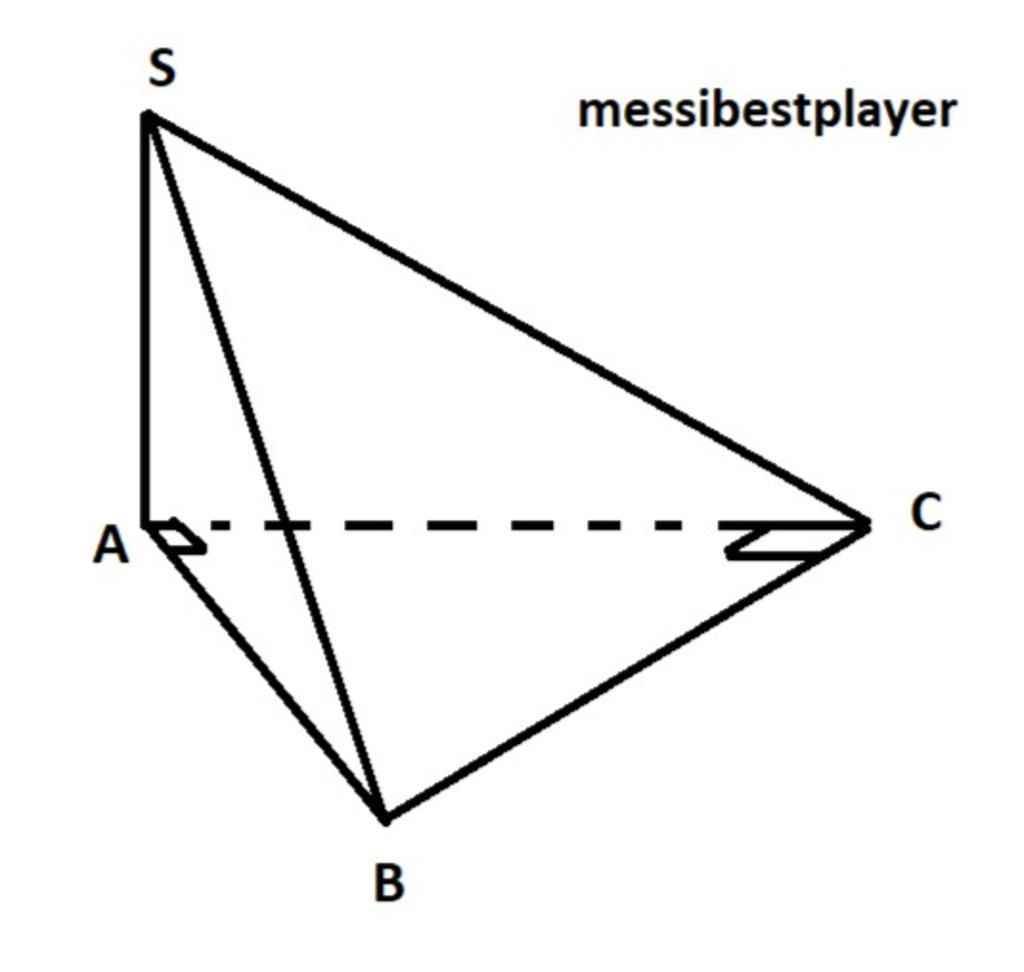
Câu 39: Xét tam giác vuông `ABC`:
Theo định lý Pitago ta có:
`AC^2 + BC^2 = AB^2; <=> BC^2 = AB^2 - AC^2 = (asqrt3)^2 - a^2= 2a^2`
`=> BC = asqrt2`
`=> S_(ABC) = AC.BC : 2 = asqrt2 . a : 2= (a^2. sqrt2)/2`
Hai mặt phẳng `SAC` và `SAB` cùng vuông góc với đáy
`=>\ SA` vuông góc với đáy; `=> SA ⊥ (ABC); => SA ⊥ AC`
`=>` Tam giác `SAC` vuông tại `A`
Theo định lý Pitago: `SA^2+AC^2 = SC^2;`
`<=> SA^2= SC^2-AC^2 =(a sqrt5)^2 - a^2 = 4a^2; => SA = 2a`
Thể tích khối chóp `S.ABC` là: `S_(ABC) . SA . 1/3`
`= (a^2. sqrt2)/2 . 2a . 1/3 = (a^3 sqrt2)/3`
`=>` Chọn `C`
tham khảo hình
38.
\(y'=\dfrac{-m-1}{\left(x-m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}-m-1< 0\\m\le2\end{matrix}\right.\) \(\Rightarrow-1< m\le2\)
\(\Rightarrow m=\left\{0;1;2\right\}\)
39.
\(\left(SAB\right)\cap\left(SAC\right)=SA\) \(\Rightarrow SA\perp\left(ABC\right)\)
\(BC=\sqrt{AB^2-AC^2}=a\sqrt{2}\)
\(SA=\sqrt{SC^2-AC^2}=2a\)
\(\Rightarrow V=\dfrac{1}{6}.SA.AC.BC=\dfrac{\sqrt{2}a^3}{3}\)