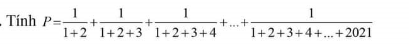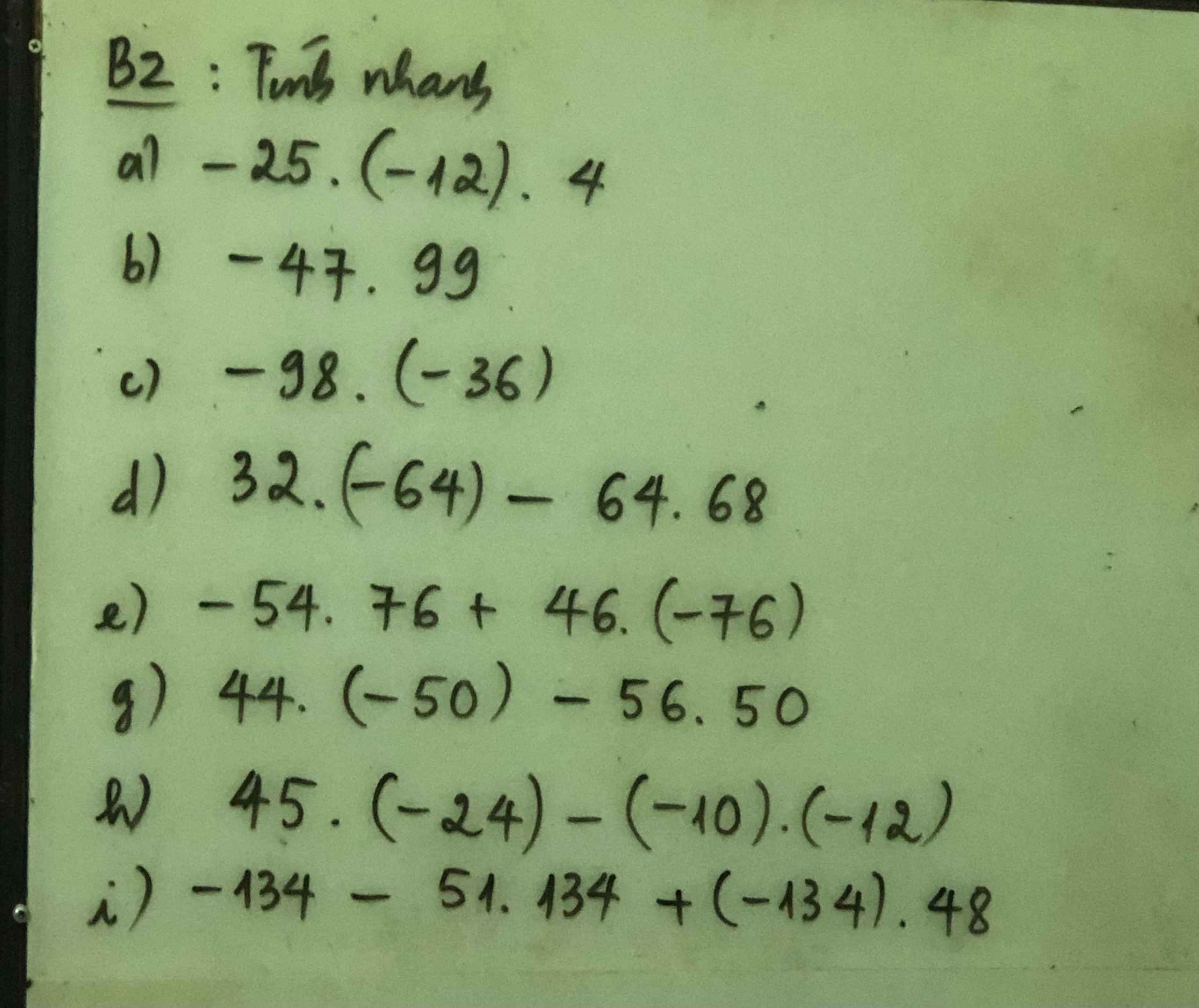1.
$A=2+2^2+2^3+2^4+...+2^{10}$
$=(2+2^2+2^3+2^4)+(2^5+2^6+2^7+2^8)+2^9+2^{10}$
$=2(1+2+2^2+2^3)+2^5(1+2+2^2+2^3)+2^9(1+2)$
$=15(2+2^5)+3.2^9$
Ta thấy $15(2+2^5)\vdots 5$ còn $3.2^9\not\vdots 5$
$\Rightarrow A\not\vdots 5$
Bài 2:
$B=2+2^2+2^3+2^4+...+2^{99}+2^{100}$
$=(2+2^2)+(2^3+2^4)+(2^5+2^6)+...+(2^{99}+2^{100})$
$=2(1+2)+2^3(1+2)+2^5(1+2)+...+2^{99}(1+2)$
$=(1+2)(2+2^3+2^5+...+2^{99})$
$=3(2+2^3+2^5+...+2^{99})\vdots 3$


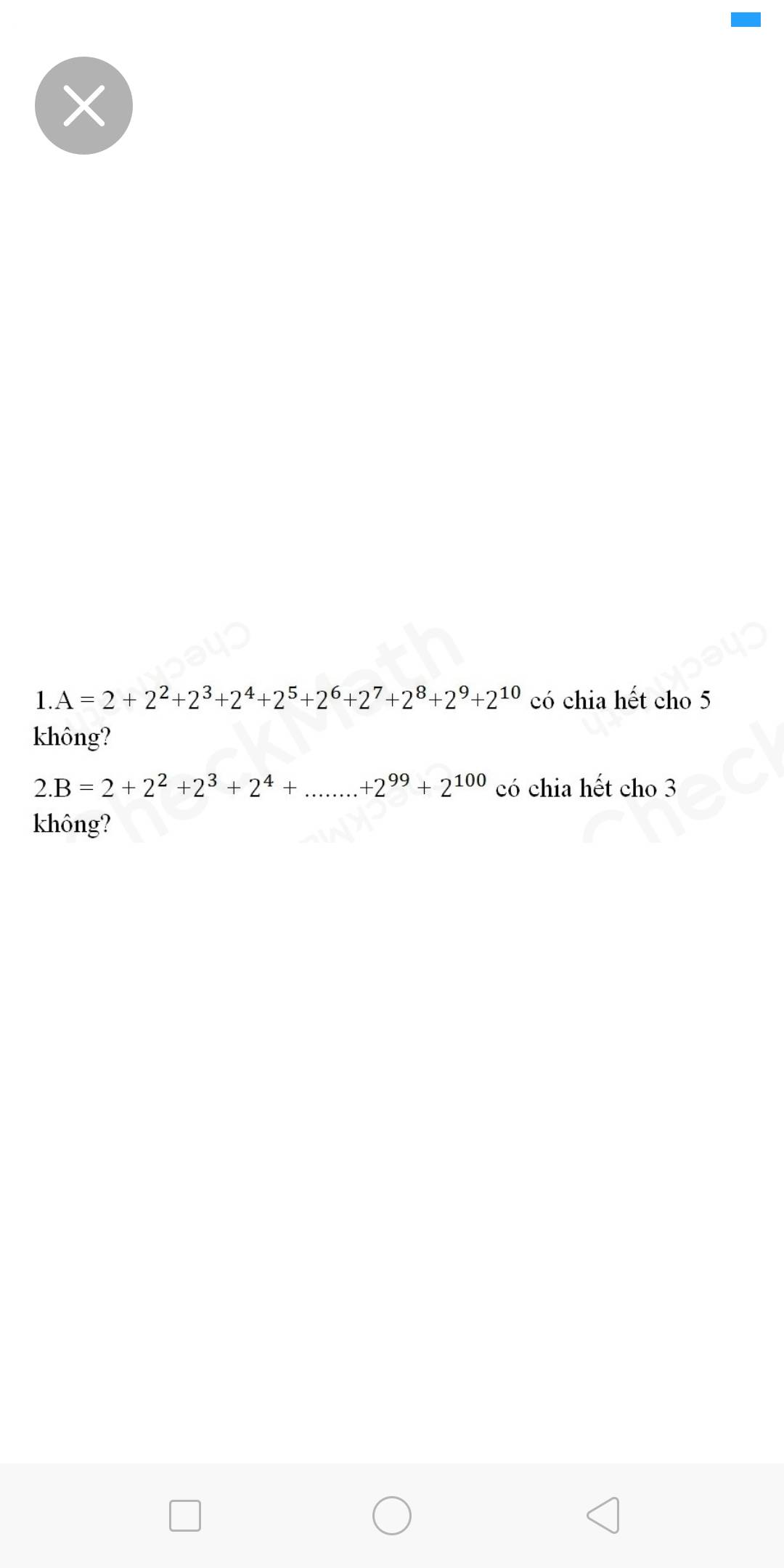








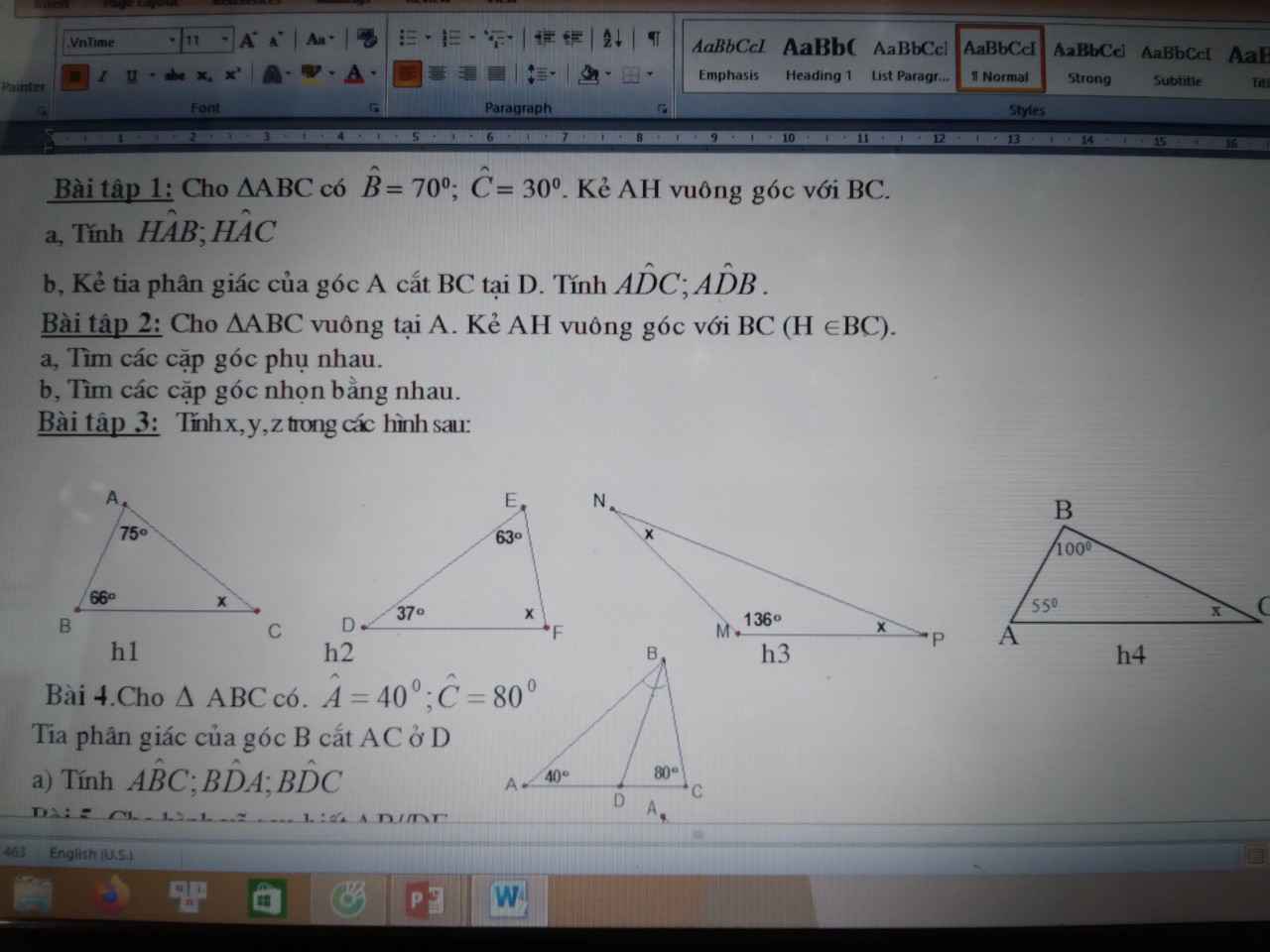 giải chi tiết giúp mik bài 3 với mik đang cần gấp
giải chi tiết giúp mik bài 3 với mik đang cần gấp