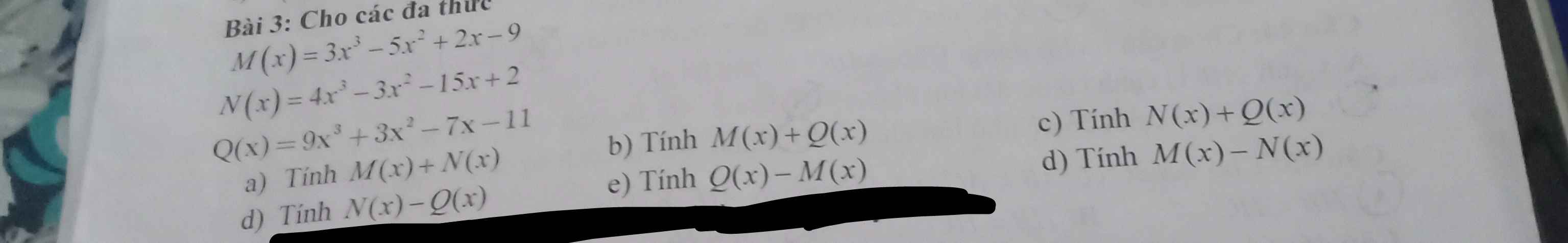\(\text{Bài 1:}M-2xyz+xy^3-x^2+5=xy^3+5xyz-4x^2+6-x^3y\)
\(\Rightarrow M=\left(xy^3+5xyz-4x^2+6-x^3y\right)+\left(2xyz+xy^3-x^2+5\right)\)
\(\Rightarrow M=xy^3+5xyz-4x^2+6-x^3y+2xyz+xy^3-x^2+5\)
\(\Rightarrow M=\left(xy^3+xy^3\right)+\left(5xyz+2xyz\right)+\left(-4x^2-x^2\right)+\left(6+5\right)-x^3y\)
\(\Rightarrow M=2xy^3+7xyz-5x^2+11-x^3y\)
\(\text{Bài 2:}P\left(x\right)=3x^3+\dfrac{1}{2}x-1-2x^2-5x^4\)
\(P\left(x\right)=5x^4+3x^3-2x^2+\dfrac{1}{2}x-1\)
\(A\left(x\right)=P\left(x\right)-Q\left(x\right)\)
\(A\left(x\right)=\left(5x^4+3x^3-2x^2+\dfrac{1}{2}x-1\right)-\left(-6x^4+3x^3-4x^2+\dfrac{1}{2}x-4\right)\)
\(A\left(x\right)=5x^4+3x^3-2x^2+\dfrac{1}{2}x-1+6x^4-3x^3+4x^2-\dfrac{1}{2}x+4\)
\(A\left(x\right)=\left(5x^4+6x^4\right)+\left(3x^3-3x^3\right)+\left(-2x^2+4x^2\right)+\left(\dfrac{1}{2}x-\dfrac{1}{2}x\right)+\left(-1+4\right)\)
\(A\left(x\right)=11x^4+2x^2-3\)

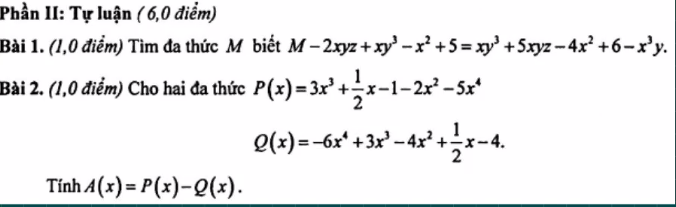 ai chỉ tui với
ai chỉ tui với