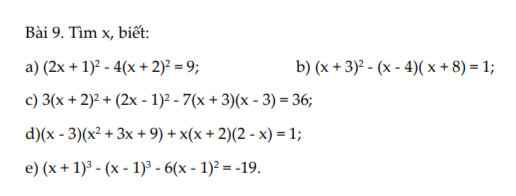a) \(\left(2x+1\right)^2-4\left(x+2\right)^2=9\\ \Rightarrow\left(2x+1\right)^2-\left[2\left(x+2\right)\right]^2=9\\ \Rightarrow\left(2x+1-2x-4\right)\left(2x+1+2x+4\right)=9\\ \Rightarrow-3\left(4x+5\right)=9\\ \Rightarrow-12x-15=9\\ \Rightarrow x=-2\)
b) \(\left(x+3\right)^2-\left(x-4\right)\left(x+8\right)=1\\ \Rightarrow x^2+6x+9-\left(x^2+4x-32\right)=1\\ \Rightarrow x^2+6x+9-x^2-4x+32=1\\ \Rightarrow2x=-40\\ \Rightarrow x=-20\)
\(a,\Rightarrow4x^2+4x+1-4x^2-16x-16=9\\ \Rightarrow-12x=24\Rightarrow x=-2\\ b,\Rightarrow x^2+6x+9-x^2-4x+32=1\\ \Rightarrow2x=-40\Rightarrow x=-20\\ c,\Rightarrow3x^2+12x+12+4x^2-4x+1-7x^2+63=36\\ \Rightarrow8x=-40\Rightarrow x=-5\\ d,\Rightarrow x^3-27+4x-x^3=1\\ \Rightarrow4x=28\Rightarrow x=7\\ e,\Rightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6=-19\\ \Rightarrow12x=-15\Rightarrow x=-\dfrac{5}{4}\)