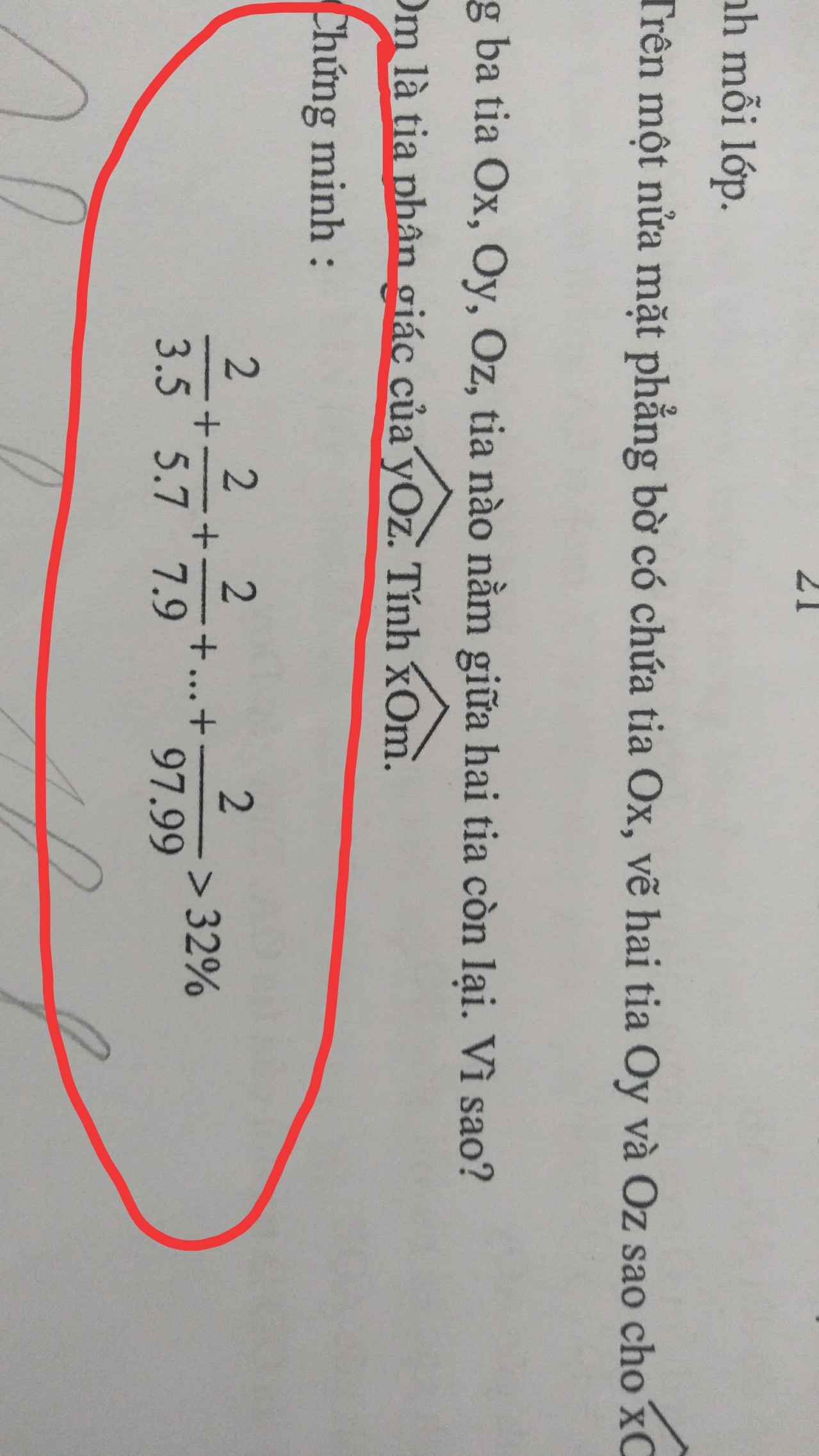Question

Ai bit lm ko

Answer 1

Lời giải:
\(A=\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+...+\frac{2}{97.99}\)

\(=\frac{5-3}{3.5}+\frac{7-5}{5.7}+\frac{9-7}{7.9}+...+\frac{99-97}{97.99}\)

\(=\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-...+\frac{1}{97}-\frac{1}{99}\)

\(=\frac{1}{3}-\frac{1}{99}=\frac{32}{99}>\frac{32}{100}=32\) %

Ta có đpcm.

Answer 2

\(\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{97.99}\)

=\(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{99}\)=\(\dfrac{1}{3}-\dfrac{1}{99}=\dfrac{32}{99}\) mà 32%=\(\dfrac{32}{100}\)

=>\(\dfrac{33}{99}>\dfrac{32}{100}\)=>\(\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{97.99}>\dfrac{32}{100}\)=>\(\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{97.99}>32\%\)

Answer 3

Giải:

\(\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{97.99}\) 

\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{99}\) 

\(=\dfrac{1}{3}-\dfrac{1}{99}\) 

\(=\dfrac{32}{99}\)