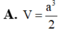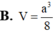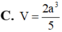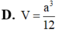Lời giải:
Do $ABC$ là tam giác đều nên $AN\perp BC$. Mà $SA\perp BC$ (do $SA\perp (ABC)$)
$\Rightarrow (SAN)\perp BC$
$AH\subset (SAN)$ nên $AH\perp BC$
Mà $AH\perp SN$
$\Rightarrow AH\perp (BC, SN)$ hay $AH\perp (SBC)$
$\Rightarrow AH\perp SC$
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B,AB=a,SA\perp AB,SC\perp BC,SB=2a.\)Gọi \(M,N\) lần lượt là trung điểm \(SA,BC\). Gọi \(\alpha\) là góc giữa \(MN\) với \(\left(ABC\right)\) .Tính \(cos\alpha\).
Cho hình chóp S.ABCD có SA \(\perp\)(ABCD) và ABCD là hình thang vuông tại A, đáy lớn AB, AB=2a, AD=CD=a. Gọi H là hình chiếu vuông góc của A lên SC và E là trung điểm của AB
a, CMR: (SCD)\(\perp\)(SAD) và AH \(\perp\)(SBC)
b, Biết góc giữa 2 mp (SCD) và (ABCD) bằng 300. Tính góc giữa 2 mp (SAD) và (SCE)?
Cho hình chóp S.ABC có SA, SB,SC đôi một vuông góc. Gọi M là trung điểm của BC. CMR
a) \(SA\perp BC\)
b) \(SA\perp SM\)
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a , SA=a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCMN bằng
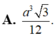
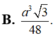
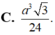
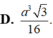
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA= 2a, S A ⊥ ( A B C ) Gọi M, N lần lượt là trung điểm SA, SB và P là hình chiếu vuông góc của A lên SC. Tính thể tích V của khói chóp S.MNP.
A. a 3 3 30
B. a 3 3 6
C. a 3 3 15
D. a 3 3 10
cho hình chóp S.ABC có đáy ABC là tam giác đều. Gọi M,N,P lần lượt là trung điểm SA,SB,SC.
tìm hình chiếu song song của đoạn thẳng NP trên (ABC) qua phép chiếu theo phương SA
Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại C và SB vuông(ABC); biết AC=a\(\sqrt{2}\), BC=a; SB=2a
a.chứng minh AC \(\perp\)(SBC)
b.gọi BH là đường cao của tam giác SBC.Chứng minh SA \(\perp\)BH
c.Tính góc giữa SA và (ABC); SA và (SBC) ; SB và (SAC)
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SA=SB=SC=a. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
Cho hình chóp S ABCD . có đáy ABCD là hình vuông tâm O , SA = SB = SC = SD .
a) Chứng minh SO \(\perp\)(ABCD ) b) Chứng minh BD\(\perp\) (SAC)
c) Gọi I là trung điểm BC. Chứng minh BC \(\perp\) (SOI)
d) Gọi K là hình chiếu vuông góc của O lên SB . Chứng minh SB \(\perp\) AK
Nhờ mọi người giải giúp em câu d ạ !! Em cảm ơn nhiều lắm ^^
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết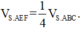 
Tính thể tích V của khối chóp S.ABC
