Các câu hỏi tương tự
a,b,cc>0, a+b+c\(\le\)3
tìm Min \(P=a^2+b^2+c^2+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
cho a,b,c là số thực dương thỏa mãn
: 2(a+b+c)+ab+bc+ca=9
tìm Max \(A=\dfrac{a+1}{a^2+10a+21}+\dfrac{b+1}{b^2+10b+21}+\dfrac{c+1}{c^2+10c+21}\)
Cho hình chóp S.ABC có đấy ABC là tam giác đều cạnh a, SA = SB = SC = 2a. Gọi o là trung điểm AC, G là trọng tâm tam giác ABC a) chứng minh (SGO) vuông góc với (ABC) b) tính góc giữa hai mặt phẳng (SAB) và (ABC) c) tính khoảng cách giữa AB và SC
Cho 2 điểm B, C cố định. Lấy điểm A thuộc đường tròn tâm (O) sao cho A, B, C không thẳng hàng. Tìm quỹ tích trọng tâm G của tam giác ABC A. Là đường tròn (O’;2R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 2 B.Là đườngtròn(O’;
1
3
R) với O’ làảnh của O qua phép vị tự tâm O tỷ số
1
3
C. Là đường tròn(O’;
1
4
R) với O’ làảnh của O qua phép vị tự tâm O tỷ số ...
Đọc tiếp
Cho 2 điểm B, C cố định. Lấy điểm A thuộc đường tròn tâm (O) sao cho A, B, C không thẳng hàng. Tìm quỹ tích trọng tâm G của tam giác ABC
A. Là đường tròn (O’;2R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 2
B.Là đườngtròn(O’; 1 3 R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 1 3
C. Là đường tròn(O’; 1 4 R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 1 4
D.Là đường tròn(O’; 4 3 R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 4 3
∆ABC có 2 điểm B, C cố định, A chạy trên đường tròn (C) tâm O bán kính R. Biết (C) không qua B, C. Gọi M là trung điểm của BC, G là trọng tâm ∆ABC. Khi A chạy trên (C) thì G chạy trên đường tròn (C’) là ảnh của (C) qua phép biến hình nào sau đây? A. Phép tịnh tiến theo vectơ
A
G
→
B. Phép vị tự tâm A tỉ số
2
3
. C. Phép vị tự tâm M tỉ số...
Đọc tiếp
∆ABC có 2 điểm B, C cố định, A chạy trên đường tròn (C) tâm O bán kính R. Biết (C) không qua B, C. Gọi M là trung điểm của BC, G là trọng tâm ∆ABC. Khi A chạy trên (C) thì G chạy trên đường tròn (C’) là ảnh của (C) qua phép biến hình nào sau đây?
A. Phép tịnh tiến theo vectơ A G →
B. Phép vị tự tâm A tỉ số 2 3 .
C. Phép vị tự tâm M tỉ số 1 3
D. Phép tịnh tiến theo vectơ M G → .
Cho tam giác ABC có AB 3a, đường cao CH a và AH a. Trên các đường thẳng vuông góc với mặt phẳng (ABC) tại A, B, C về cùng một phía của mặt phẳng (ABC) lấy các điểm A’, B’, C’sao cho AA’ 3a, BB’ 3a, CC’ a. Tính diện tích tam giác A’B’C’.
Đọc tiếp
Cho tam giác ABC có AB = 3a, đường cao CH = a và AH = a. Trên các đường thẳng vuông góc với mặt phẳng (ABC) tại A, B, C về cùng một phía của mặt phẳng (ABC) lấy các điểm A’, B’, C’sao cho AA’ = 3a, BB’ = 3a, CC’ = a. Tính diện tích tam giác A’B’C’.
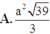
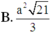
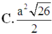
Câu 25: Cho tứ diện
ABCD
và đặt
AB a AC b AD c = = =
, ,
. Gọi
M
là trung điểm của cạnh
CD
. Véc tơ
2BM
bằng:
A.
− + + 2a b c . B.
− + + 2abc . C. - − + + abc . D.
a b c − +
4: Cho lăng trụ
ABC A B C . ' ' '
có
M N P , ,
lần lượt là trung điểm của
AB AC CC , , '.
a) Chứng minh rằng
(NMP AB C )/ /( ' ').
b) Gọi
K
là điểm thỏa mãn
BK xBC =
'
. Tìm
x
để
MK AB C / / ' ' .
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:A(n) : “nếu a và b là những số nguyên dương mà max{a,b} n thì a b”Chứng minh :Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} 1 thì a b”Mệnh đề A(1) đúng vì max{a,b} 1 và a,b là những số nguyên dương thì a b 1.Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1Bước 3: xét max{a,b} k+1 ⇒max{a-1,b-1} k+ 1-1 kDo a(k) là mệnh đề đúng nên a- 1 b-1 ⇒ a b⇒...
Đọc tiếp
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?
Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:
A(n) : “nếu a và b là những số nguyên dương mà max{a,b} = n thì a = b”
Chứng minh :
Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} = 1 thì a = b”
Mệnh đề A(1) đúng vì max{a,b} = 1 và a,b là những số nguyên dương thì a= b =1.
Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1
Bước 3: xét max{a,b} = k+1 ⇒max{a-1,b-1} = k+ 1-1 = k
Do a(k) là mệnh đề đúng nên a- 1= b-1 ⇒ a= b⇒ A(k+1) đúng.
Vậy A(n) đúng với mọi n ∈N*
A. Bước 1
B. Bước 2
C. Bước 3
D. Không có bước nào sai