Do BC là cạnh chung
CA = CA' (gt)
Nên cần có thêm góc xen giữa là ∠ACB = ∠A'CB
Mà theo đề bài ta chỉ có ∠ABC = ∠A'BC
Do đó không thể kết luận ∆ABC = ∆A'BC theo trường hợp canh-góc-cạnh
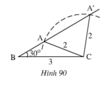
Không.
Lý do: Trong trường hợp bằng nhau Cạnh – Góc – Cạnh (CGC / SAS), góc phải là góc xen giữa hai cạnh đã biết.
Ở đây bạn biết:
\(B C = 3\) cm\(C A = C A^{'} = 2\) cm\(\hat{A B C} = \hat{A^{'} B C} = 30^{\circ}\)Nhưng góc đã cho là \(\hat{A B C}\), tức là góc tại B, không phải góc xen giữa \(B C\) và \(C A\).
Góc xen giữa \(B C\) và \(C A\) phải là \(\hat{B C A}\).
Vì vậy không thỏa mãn điều kiện CGC, nên không thể kết luận
\(\Delta A B C = \Delta A^{'} B C\) theo trường hợp bằng nhau cạnh – góc – cạnh.
Đáp án: Không.