\(a;b;c\in\left[0;1\right]\Rightarrow\left\{{}\begin{matrix}a-1\le0\\b-1\le0\\c-1\le0\end{matrix}\right.\) \(\Rightarrow\left(a-1\right)\left(b-1\right)\left(c-1\right)\le0\)
\(S=a+b+c-ab-bc-ca=\left(abc-ab-bc-ca+a+b+c-1\right)+1-abc\)
\(S=\left(1-a\right)\left(1-b\right)\left(1-c\right)+1-abc\le1-abc\le1\)
\(S_{max}=1\) khi \(\left(a;b;c\right)=\left(0;0;1\right);\left(0;1;1\right)\) và các hoán vị







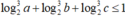 . Khi biểu thức
. Khi biểu thức