Kẻ đường cao AH
Ta có: AD=AB(=x) \(\Rightarrow\Delta ABD\) cân tại A
\(\Rightarrow\) AH cũng là đường trung trực
\(\Rightarrow\) DH=HB=9m
\(\Rightarrow CH=AD+DH=7+9=16\left(m\right)\)
Xét \(\Delta ABC\) vuông tại A, đường cao AH có:
\(AH^2=BH\cdot CH\) (HTL)
\(\Rightarrow AH=\sqrt{9\cdot16}=12\) (m)
Xét \(\Delta AHB\) vuông tại H có:
\(AB^2=AH^2+HB^2\) (ĐL Py-ta-go)
\(\Rightarrow AB=\sqrt{12^2+9^2}=15\) (m)
\(\Rightarrow x=15\left(m\right)\)

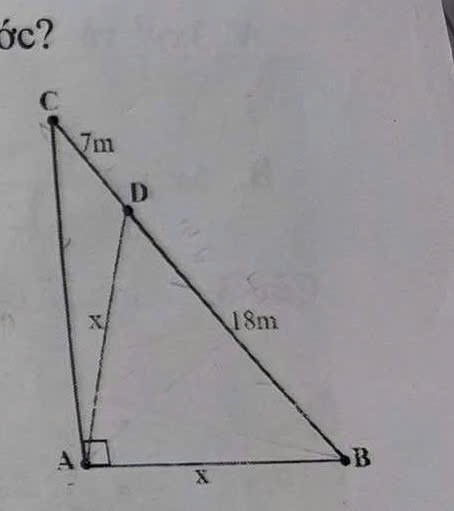 AB vuông góc với AC,AD=AB=x tìm x ,cứu với ạ mình sẽ tim ạ
AB vuông góc với AC,AD=AB=x tìm x ,cứu với ạ mình sẽ tim ạ











