a) Cách vẽ
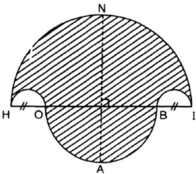
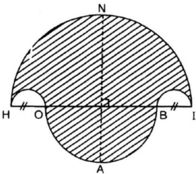
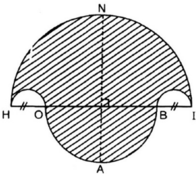
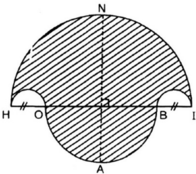
- Vẽ nửa đường tròn đường kính HI = 10cm, tâm M.
- Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.
- Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).
- Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.
b)
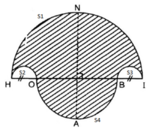
Diện tích miền gạch sọc bằng:
S = S 1 − S 2 − S 3 + S 4
với:
+ S 1 là nửa đường tròn đường kính HI
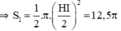
+ S 2 ; S 3 là nửa đường tròn đường kính HO và BI.
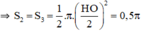
+ Ta tính OB:
Ta có: HO+ OB + BI = HI
⇔ 2+ OB + 2= 10 nên OB = 6
+ S4 là nửa đường tròn đường kính OB
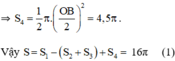
c)Ta có: 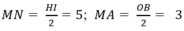
Do đó, NA = MN+ MA= 8
Diện tích hình tròn đường kính NA bằng : π 4 2 = 16 π ( c m 2 ) ( 2 )
so sánh (1) và (2) ta thấy hình tròn đường kính NA có cùng diện tích với hình HOABINH.