a, AC = 4cm => BC = 4 3 cm
=> R = 4cm => C = 8πcm, S = 16π c m 2
b, ∆AOC đều => A O C ^ = 60 0
=> C O D ^ = 120 0 => l C A D ⏜ = π . 4 . 120 180 = 8 π 3 cm
=> S = 8 π 3 . 4 2 = 16 π 3 c m 2
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD R (C thuộc cung AD). Nối AC và BD cắt nhau tại Ma, Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc
A
M
B
^
không đổib, Cho
A
B
C
^
30...
Đọc tiếp
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD = R (C thuộc cung AD). Nối AC và BD cắt nhau tại M
a, Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc A M B ^ không đổi
b, Cho A B C ^ = 30 0 , tính độ dài cung nhỏ AC và diện tích hình viên phân giói hạn bởi dây AC và cung nhỏ AC
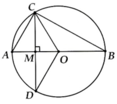
Cho đường tròn (O), đường kính AB, CD. AB vuông góc với CD. Lấy điểm E thuộc cung nhỏ BD (\(E\ne B,D\)). CE cắt AB tại M.
a) Chứng minh: tứ giác OMED nội tiếp
b) So sánh góc MAE và góc MDE
c) Giả sử gócMAE=20º. R=3cm. Tính độ dài cung nhỏ BE và diện tích hình quạt tròn OBE
Cho đường tròn (O; R), đường kính AB cố định. Gọi M là trung điểm đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyên động trên cung lớn CD (E khác A). Nôi AE cắt CD tại K. Nối BE cắt CD tại Ha, Chứng minh bốn điểm B, M, E, K thuộc một đường trònb, Chứng minh AE.AK không đổic, Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
Đọc tiếp
Cho đường tròn (O; R), đường kính AB cố định. Gọi M là trung điểm đoạn OB. Dây CD vuông góc với AB tại M. Điểm E chuyên động trên cung lớn CD (E khác A). Nôi AE cắt CD tại K. Nối BE cắt CD tại H
a, Chứng minh bốn điểm B, M, E, K thuộc một đường tròn
b, Chứng minh AE.AK không đổi
c, Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
Cho đường tròn (7; 2cm). Vẽ bán kính IA và IB sao cho
A
I
B
^
120
0
. Hãy tính:a, Độ dài cung nhỏ ABb, Diện tích hình quạt tròn giới hạn bởi cung nhỏ AB và hai bán kính IA, IB
Đọc tiếp
Cho đường tròn (7; 2cm). Vẽ bán kính IA và IB sao cho A I B ^ = 120 0 . Hãy tính:
a, Độ dài cung nhỏ AB
b, Diện tích hình quạt tròn giới hạn bởi cung nhỏ AB và hai bán kính IA, IB
Cho đường tròn tâm O đường kính AB = 6cm. Vẽ hai tiếp tuyến Ax , By của đường tròn. Qua 1 điểm M thuộc nửa đường tròn sao cho MAB = 55 độ vẽ tiếp tuyến thứ ba cắt Ax và By lần lượt tại E và F
a, Chứng minh tứ giác AEMO nội tiếp
b, Tính độ dài cung nhỏ MB và diện tích hình quạt tròn giới hạn bởi cung nhỏ MB
c, Tính độ dài đoạn thẳng AM
Cho đường tròn tâm O đường kính AB = 6cm. Vẽ hai tiếp tuyến Ax , By của đường tròn. Qua 1 điểm M thuộc nửa đường tròn sao cho MAB = 55 độ vẽ tiếp tuyến thứ ba cắt Ax và By lần lượt tại E và F
a, Chứng minh tứ giác AEMO nội tiếp
b, Tính độ dài cung nhỏ MB và diện tích hình quạt tròn giới hạn bởi cung nhỏ MB
c, Tính độ dài đoạn thẳng AM
Cho đương tròn (O;R), đường kính AB cố định. Gọi M là trung điểm của đoạn OB. Dây CD vuông góc AB tại M. Điểm E chuyển độn trên cung lớn CD(E khác A). Nối AE cắt CD tại K. Nối BE cắt CD tại H
a, C/M rằng 4 điểm B,M, E, K thuộc 1 dường tròn
b, C/M AE.AK không đổi
c, Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
Cho đường tròn (O; R), kính AB cố định. Gọi M là trung điểm của OB. Dây CD vuông góc với AB tại M. Điểm E chuyển động trên cung lớn CD. Nối AE cắt CD tại K. Nối BE cắt CD tại H.
a) C/m: AE.AK không đổi
b) Tính theo R diện tích hình quạt tròn giới hạn bởi OB, OC và cung nhỏ BC
c) C/m: tâm I của đường tròn ngoại tiếp tam giác BHK luôn thuộc một đường thẳng cố định.
1/ Cho đường tròn (O) đường kính AB và 1 điểm C trên đường tròn.Từ O kẻ 1 đường thảng song song với dây AC , đường thảng này cắt tiếp tuyến tại B của đường tròn ở điển C A) CM: OD là phân giác của góc BOC b) CN: CD là tiếp tuyến của đường tròn2/ Cho đường tròn (O;R), H là điểm bên trong đường tròn (H không trùng với O). Vẽ đưởng kính AB đi qua H (HB HA). Vẽ dây CD vuông góc với AB tại H. CMR:a) Góc BCA 90 độ b) CH . HD HB . HA c) Biết OH R/2. Tính diện tích tam giác ACD theo...
Đọc tiếp
1/ Cho đường tròn (O) đường kính AB và 1 điểm C trên đường tròn.Từ O kẻ 1 đường thảng song song với dây AC , đường thảng này cắt tiếp tuyến tại B của đường tròn ở điển C A) CM: OD là phân giác của góc BOC b) CN: CD là tiếp tuyến của đường tròn
2/ Cho đường tròn (O;R), H là điểm bên trong đường tròn (H không trùng với O). Vẽ đưởng kính AB đi qua H (HB < HA). Vẽ dây CD vuông góc với AB tại H. CMR:
a) Góc BCA = 90 độ b) CH . HD = HB . HA c) Biết OH = R/2. Tính diện tích tam giác ACD theo R
3/ Cho tam giác MAB, vẽ đường tròn (O) đường kính AB cắt MA ở C, cắt MB ở D. Kẻ AP vuông góc CD , BQ cuông góc CD. Gọi H là giao điểm AD và BC. CM:
a) CP = DQ b) PD . DQ = PA . BQ và QC . CP = PD . QD c) MH vuông góc AB\
4/ Cho đường tròn (O;5cm) đường kính AB, gọi E là 1 điểm trên AB sao cho BE = 2cm.Qua trung điểm kH của đoạn AE vẽ dây cung CD vuông góc AB.
a) Tứ giác ACED là hình gì? Vì sao? b)Gọi I là giao điểm của DE với BC. CMR:I thuộc đường tròn (O') đường kính EB
c) CM HI là tiếp điểm của đường tròn (O') d) Tính độ dài đoạn HI
5/ Cho đường tròn (0) đường kính AB = 2R. Gọi I là trung điểm của AO, qua I kẻ dây CD vuông góc với OA.
a) Tứ giác ACOD là hình gì? tại sao?
b) CM tam giác BCD đều
c) Tính chu vi và diện tích tam giác BCD theo R
6/ Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 9cm; BC = 15cm
a) Tính độ dài các cạnh AC, AH, BH, HC
b) Vẽ đường tròn tâm B, bán kính BA. Tia AH cắt (B) tại D. CM: CD là tiếp tuyến của (B;BA)
c) Vẽ đường kính DE. CM: EA // BC
d) Qua E vẽ tiếp tuyến d với (B). Tia CA cắt d tại F, EA cắt BF tại G. CM: CF = CD + EF và tứ giác AHBG là hình chữ nhật
7/ Cho đường tròn (O) đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. gọi E là giao điểm của AC và BM.
a) CMR: NE vuông góc AB
b) Gọi F là điểm đối xứng với E qua M. CMR: FA là tiếp tuyến của đường tròn (O)
c) CM: FN là tiếp tuyến của đường tròn (B;BA)
8/ Cho nửa đường tròn (O), đường kính AB.Từ một điểm M trên nửa đường tròn ta vẽ tiếp tuyến xy. Từ A ta vẽ AD vuông góc với xy tại D
a) CM: AD // OM
b) Kẻ BC vuông góc với xy tại C. CMR: MC = MD