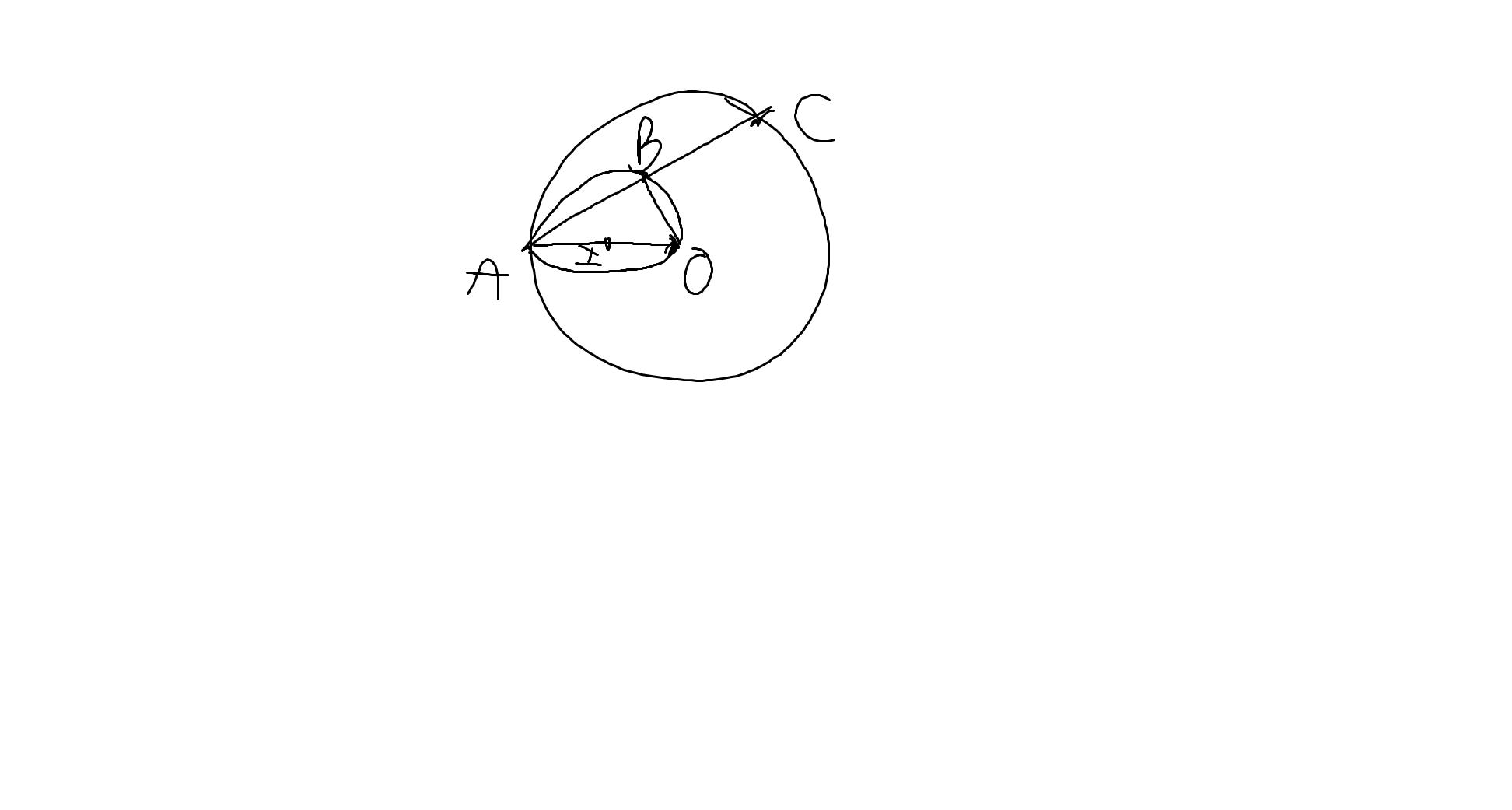
Xét (I) có
ΔBOA nội tiếp
OA là đường kính
Do đó: ΔBOA vuông tại B
=>OB\(\perp\)AC tại B
ΔOAC cân tại O
mà OB là đường cao
nên B là trung điểm của AC
=>\(AB=\dfrac{AC}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Cho đường tròn tâm O đường kính AB. Trên bán kính OA, lấy điểm C tùy ý (C khác O và A). Vẽ đường tròn tâm J đường kính AC. Gọi I là trung điểm BC. Qua I vẽ dây cung MN vuông góc BC; AM cắt đường tròn tâm J tại E.
a/ CM CIME nội tiếp.
b/ CM BMCN là hình thoi. Từ đó suy ra ba điểm E, C, N cùng thuộc một đường thẳng.
c/ CM IE là tiếp tuyến của đường tròn tâm J.
d/ Đường tròn tâm M bán kính MI cắt đường tròn tâm O tại P và Q, Gọi H là giao điểm của PQ và MN. Tính tỉ số HM/HN
Cho đường tròn tâm O đường kính AB. Vẽ đường tròn tâm I đg kính OA bán kính OC của đg tròn tâm O cắt đg trong tâm I tại D. Vẽ CH vuong goc AB (C thuộc đg tròn tâm O, đg kính AB). C/m rằng ACDH là hình thang cân. Vẽ hình giúp e với luôn đk ạ
Cho đường tròn tâm O, bán kính R, đường kính AB, vẽ đường tròn tâm I, đường kính OA. a. Chm 2 đường tròn tâm O và tâm I tiếp xúc nhau, b. Dây AC của đường tròn tâm O cắt tâm I tại D. Chm ID//OC. c. Biết AC = R căn 3 . Tính theo R , diện tích ODCB
Bài 1: Từ điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B,C là hai tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).
a) cm: A,B,O,C cùng thuộc một đường tròn.
b) cm: OA vuông BC tại H và OD2 = OH.OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA.
c) cm: BC trùng với tia phân giác của góc DHE.
d) Từ D kẻ đường thẳng song song với BE, đường thẳng này cắt AB, AC lần lượt tại M và N. cm: D là trung điểm MN.
Bài 2: Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O,R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc vs CD tại H.
a) cm: A,B,O,C cùng thuoojcj một đường tròn. Xác định tâm và bán kính của đường tròn đó.
b) cm: AO vuông góc vs BC. Cho biết R=15cm, BC=24cm. Tính AB, OA.
c) cm: BC là tia phân giác của góc ABH.
d) Gọi I là giao điểm của AD và BH, E là giao điểm của BD và AC. cm: IH=IB.
Cho đường tròn (O;R), đường kính AC, trên bán kính OA lấy điểm B tùy ý (B khác O và A). Vẽ đường tròn tâm N đường kính AB. Gọi M là trung điểm của BC. Qua M vẽ dây DE vuông góc với BC, AD cắt (N) tại I.
a. CM tứ giác BMDI nội tiếp
b. 3 điểm I, B, E thẳng hàng
c. MI là tiếp tuyến của (N)
d. đường tròn tâm D bán kính DM cắt (O) tại P và Q. CM PQ qua trung điểm của MD.
Giúp tớ câu d với
Giúp mình với!!!
Cho nửa đường tròn tâm O đường kính AB=2R (R>9). Trên bán kính OA lấy hai điểm C và D sao cho AC=6; AD=9. Đường thẳng vuông góc với AB tại D cắt nửa đường tròn tại E. Điểm F thuộc nửa đường tròn sao cho ^ACF=^DCE. Đường tròn tâm I bán kính r tiếp xúc với 2 cạnh của góc ECF và tiếp xúc trong với đường tròn tâm O. Tính r.
BÀI 1 cho nửa đường tròn tâm o đường kính AB CD là dây bất kì khác AB kẻ AE và BF vuông góc với CD chứng minh CE=DF
BÀI 2 cho nữa đường tròn O đường kính AB trên AB lấy hai điểm C và D sao cho OC=OD .từ C và D kẻ hai tia song song nhau cắt nửa đường tròn tại E và F chứng minh EF vuông góc với CE và DF
Bài 3 cho đường tròn o có bán kính OA =11 cm điểm M thuộc OA và cách o là 7 cm qua M kẻ dây CD có độ dài 18 cm tính độ dài MC, MD
Bài 4 cho tam giác ABC cân nội tiếp đường tròn O
A chừng minh AO là đường trung trực của BC
B tính đường cao AH của tam giác ABC biết AC=40cm bán kình đường tròn O = 25 cm
Bài 5 cho đường tròn O đường kính AB dây CD vuông góc AB tại điểm M ,M thuộc OA
gọi I là một điểm thuộc OB .Các tia CI ,DI theo thứ tự cắt dường tròn tại E và F
A Cm tam giác ICD cân
gọi H,K theo thứ tự là chân các đường vuông góc kẻ từ O đến CE DF so sánh OH và OK
giúp mình với mình cảm ơn nhiều
Bài 1: Cho đường tròn (O), đường kính AB, dây CD vuông góc với AB tại điểm H thuộc bán kính OA. Gọi M là điểm thuộc bán kính OB, E và F theo thứ tự là giao điểm của CM và DM với đường tròn (E khác C, F khác D). Chứng minh rằng: a) MC = MD b) ME = MF
giúp mình vs . tại mình cần gấp . cẩm ơn mn nhiều
Bài 1: Cho đường tròn (O), đường kính AB, dây CD vuông góc với AB tại điểm H thuộc bán kính OA. Gọi M là điểm thuộc bán kính OB, E và F theo thứ tự là giao điểm của CM và DM với đường tròn (E khác C, F khác D). Chứng minh rằng: a) MC = MD b) ME = MF
Bài 2: Cho đường tròn (O) đường kính AB. Vẽ các dây BC, BD thuộc hai nửa mặt phẳng đối nhau bờ AB sao cho BD > BC. So sánh độ dài hai dây AD và AC.
Bài 3. Cho đường tròn (O), hai dây AB và AC vuông góc với nhau có độ dài theo thứ tự bằng 10cm và 24cm. a) Tính khoảng cách từ tâm đến mỗi dây b) chứng minh rằng ba điểm B, O, C thẳng hàng.
Bài 4. Cho đường tròn (O), hai dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Trên tia đối của tia AB lấy điểm E sao cho AE = BM. Trên tia đối của tia CD lấy điểm F sao cho CF = DM. Chứng minh rằng OE = OF.
Bài 5. Cho đường tròn (O), hai dây AB và CD có AB > CD, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. So sánh các độ dài MH và MK.
giải giúp mình vs ạ . tạo mình đang cần gấp . cảm ơn nha
Cho đường tròn (O) có đường kính AB = 2R, dây CD vuông góc với OA tại trung điểm M của OA. Tieeso tuyến tại C của (O) cắt OA tại N.
a) Chứng minh tứ giác ACOD là hình thoi. Tính số đo góc COA và độ dài CN theo R.
b) Vè đường tròn tâm D bán kính DM cắt đường tròn (O) tại E và F. Vẽ đường kính DP của (O), DP cắt BC tại I và cắt FE tại H. Chứng minh I là trung điểm BC và BC song song với FE.
c) Gọi K là trung điểm DM. Chứng minh E, K, F thẳng hàng.
mọi người cho mình xin câu b ý 2 và câu c thôi ạ, mình cảm ơn nhiều
