Question

2x(x-5)-(3+2x)=26

(2x-3)^2 -(x+5)^2 =0

(x-1)^3 -x(x-2)62 -(x-2)=0

(ko dùng delta ạ ;-;)

Answer 1

2x(x - 5) - (3 + 2x) = 26

2x² - 10x - 3 - 2x - 26 = 0

2x² - 12x - 29 = 0

2x² - 2.2.x.3 + 2.9 - 29 - 2.9 = 0

2(x² - 2.x.3 + 9) - 47 = 0

2(x - 3)² = 47

*)

*)

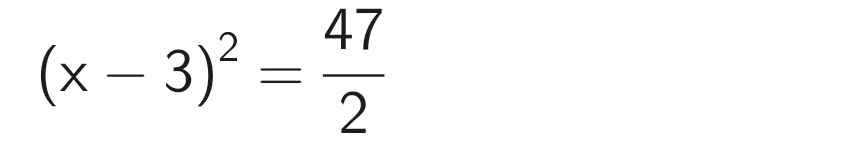
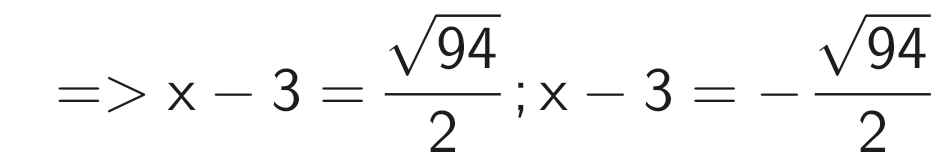
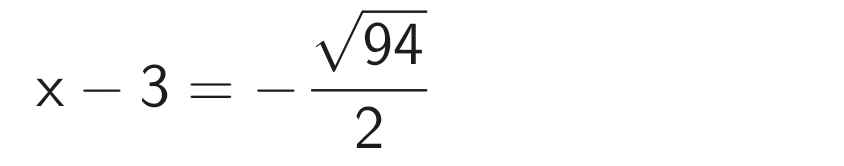
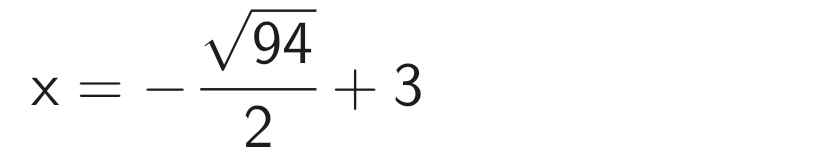
Vậy:

  

Answer 2

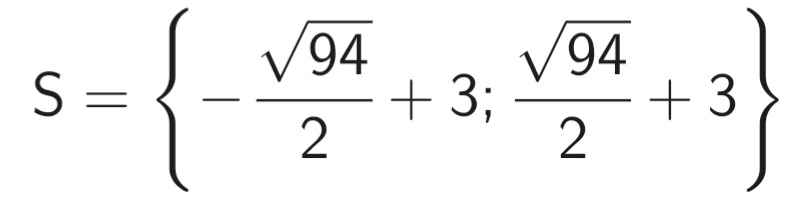
$#flo$

`2x(x-5) - (3+2x) = 26`

`=>2x^2 - 10x -3 -2x = 26`

`=> 2x^2 -12x - 3 =26`

`=> 2x^2 - 12x  -3 - 26 = 0`

`=>2x^2 - 12x - 29 = 0`

`=> 2(x^2 - 6x - 29/2) = 0`

`=>   x^2 - 6x - 29/2 = 0`

`=> x^2 -2x.3 + 9 - 47/2 = 0`

`=> (x-3)^2 -47/2 = 0`

`=>(x-3)^2 = 47/2`

TH1:

\(x-3=\dfrac{\sqrt{94}}{2}\)

`=> x` = \(\dfrac{\sqrt{94}}{2}+3\)

TH2:

`x-3 = ` \(\dfrac{-\sqrt{94}}{2}\)

`=> x = \(\dfrac{-\sqrt{94}}{2}+3\)

`2) (2x-3)^2 - (x+5)^2 = 0`

`=> (2x-3-x-5)(2x-3+x+5) = 0`

`=> (x-8)(3x+2)=0`

\(\Rightarrow\left[{}\begin{matrix}x-8=0\\3x+2=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-\dfrac{2}{3}\end{matrix}\right.\)

 

Answer 3

(2x - 3)² - (x + 5)² = 0

(2x - 3 - x - 5)(2x - 3 + x + 5) = 0

(x - 8)(3x - 2) = 0

x - 8 = 0 hoặc 3x - 2 = 0

*) x - 8 = 0

x = 8

*) 3x - 2 = 0

3x = 2

x = 2/3

Vậy S = {2/3; 8}