Các câu hỏi tương tự
Câu 1. Cho hình chóp S ABC . có SA vuông góc với ABC và đáy ABC đều cạnh a. Biết SA3a/2.Gọi H là trung điểm của BC.a. Tính góc giữa hai mặt phẳng SBC và ABC ?b. Tính diện tích của tam giác ABC từ đó suy ra diện tích tam giác SBC ?c. Chứng minh SBC vuông góc với SAH Câu 2. Cho hình chóp tam giác đều S ABC . có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi mặt bên và mặt đáy
Đọc tiếp
Câu 1. Cho hình chóp S ABC . có SA vuông góc với ABC và đáy ABC đều cạnh a. Biết SA=3a/2.Gọi H là trung điểm của BC.
a. Tính góc giữa hai mặt phẳng SBC và ABC ?
b. Tính diện tích của tam giác ABC từ đó suy ra diện tích tam giác SBC ?
c. Chứng minh SBC vuông góc với SAH
Câu 2. Cho hình chóp tam giác đều S ABC . có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi mặt bên và mặt đáy
cho hình chóp S.ABC có đáy là tam giác ABC vuông tai B; SA = AB = BC = a và SA vuông góc (ABC). Chứng minh rằng:
a) BC vuông góc (SAB)
b) BC vuông góc SA
c) tìm góc giữa AC và (SBC)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , SA![]() (ABC) . Kẻ AH , AK lần lượt vuông góc với SB , SC tại H và K , có SA = AB = a .
(ABC) . Kẻ AH , AK lần lượt vuông góc với SB , SC tại H và K , có SA = AB = a .
1) Chứng minh tam giác SBC vuông .
2) Chứng minh tam giác AHK vuông và tính diện tích tam giác AHK .
3) Tính góc giữa AK và (SBC) .
Cho hình chóp S.ABC SA vuông góc với đáy ABC, SA=2a
Xđịnh góc giữa 2 mp (SBC) và ( ABC) .
Biết tam giác ABC vuông tại B, cạnh AB=a
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C ; SA vuông góc với đáy; SC a. Gọi
α
là góc giữa hai mặt phẳng (SBC) và (ABC). Tính để thể tích khối chóp S.ABC lớn nhất
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C ; SA vuông góc với đáy; SC = a. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC). Tính để thể tích khối chóp S.ABC lớn nhất
![]()
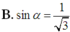
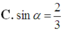
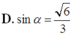
Cho hình chóp S.ABC có đáy ABC là tam giác đều, I là trung điểm của BC, SA vuông góc với (ABC). Gọi H, O lần lượt là trực tâm của tam giác SBC, ABC, K là giao điểm của hai đường thẳng SA và OH. Chứng minh rằng:
a) OH vuông góc với (SBC)
b) SO vuông góc với IK.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông (ABC) SA= a cân 3; AB=a
A: Chứng minh (SAB) vuông (SAC)
B: Gọi M là trung điểm của BC, chứng minh BC vuông góc vs SM
C: Tính góc giữa SC và (ABC
Cho hình chóp S.ABC có SA vuông góc với (ABC), tam giác ABC là tam giác vuông cân tại A, AB 2a, góc giữa (SBC) và mặt đáy bằng
60
0
. Thể tích khối chóp S.ABC là:
A
.
125
2
a
3
6
B
.
3
6...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với (ABC), tam giác ABC là tam giác vuông cân tại A, AB = 2a, góc giữa (SBC) và mặt đáy bằng 60 0 . Thể tích khối chóp S.ABC là:
A . 125 2 a 3 6
B . 3 6 a 3 4
C . 16 2 a 3 3
D . 2 6 a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy.
a) Chứng minh tam giác SBC vuông
b) Gọi H là chân đường cao vẽ từ B của tam giác ABC.
Chứng minh (SAC) ⊥ (SBH)
c) Cho AB = a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC) A. 300 B. 450 C. 600 D. 900
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)
A. 300
B. 450
C. 600
D. 900








