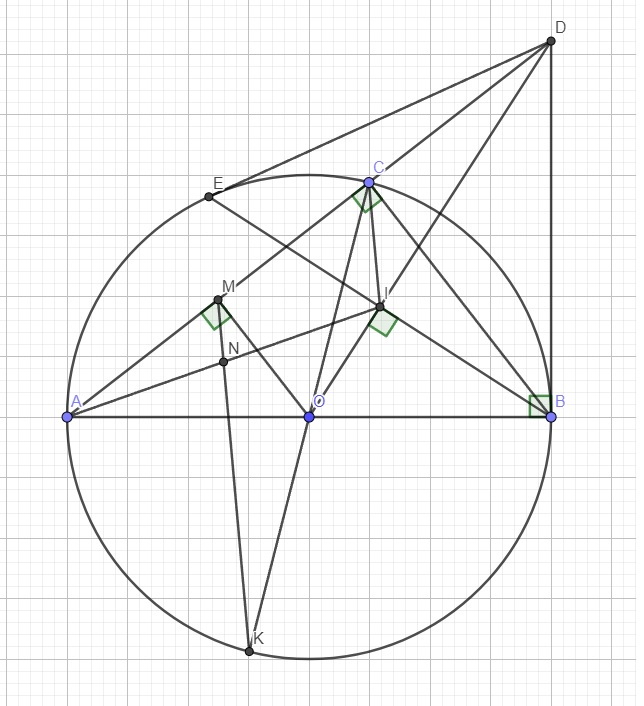
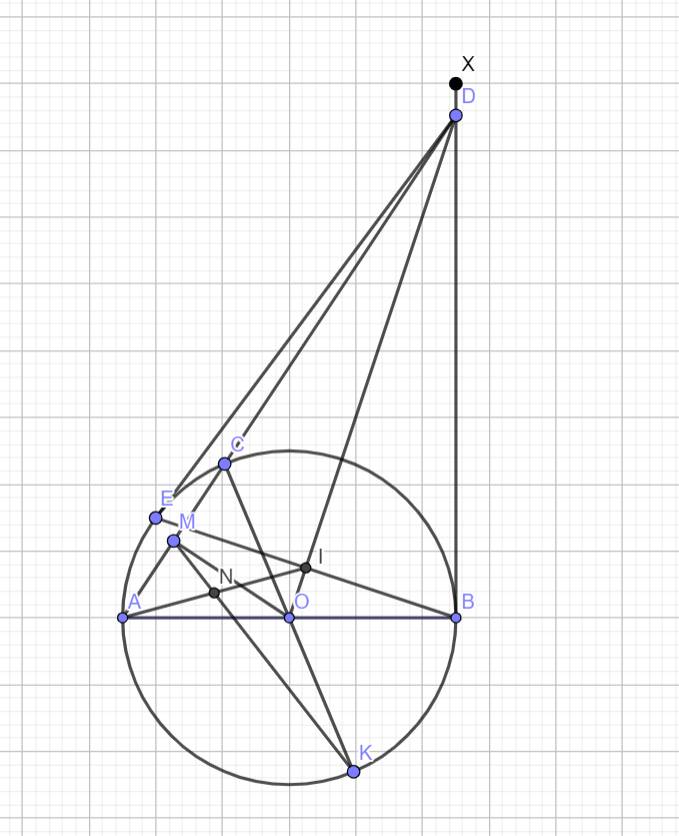
2) Cho đường tròn (O;R) đường kính AB, lấy điểm C thuộc đường tròn (O) (C khác A và B). Trên cùng một nửa mặt phẳng bờ AB chứa điểm C, kẻ tiếp tuyến Bx với đường tròn (O) cắt AC tại D. Từ D kẻ tiếp tuyến DE với (O) (E là tiếp điểm khác B). Gọi I là giao điểm của OD và BE. 1) Cm bốn điểm B,O,E,D cùng thuộc 1 đg tròn. 2) Kẻ đường kính CK của đường tròn (O), OM vuông góc AC tại M, KM cắt AI tại N. Cm: N là trung điểm của AI. 1) Một người A đang ở trên khinh khí cầu ở độ cao 150m nhìn thấy 1 vật B trên mặt đất cách hình chiếu của khí cầu xuống đất một khoảng 285m. Tính góc hạ của tia AB. Nếu khinh khí cầu tiếp tục bay lên thẳng đứng thì góc hạ của tia AB là 46 độ thì độ cao của khinh khí cầu là bao nhiêu? ( Làm tròn đến mét).
2.
Do BD là tiếp tuyến của (O) tại D \(\Rightarrow\widehat{OBD}=90^0\)
Do DE là tiếp tuyến của (O) tại E \(\Rightarrow\widehat{OED}=90^0\)
\(\Rightarrow\) B và E cùng nhìn OD dưới 1 góc vuông nên 4 điểm B, O, E, D cùng thuộc đường tròn đường kính OD
b.
Ta có \(DB=DE\) (t/c hai tiếp tuyến cắt nhau)
\(OB=OE=R\)
\(\Rightarrow OD\) là trung trực của BE \(\Rightarrow OD\perp BE\) tại I
Do AB là đường kính \(\Rightarrow\widehat{ACB}=90^0\) (góc nt chắn nửa đường tròn)
Áp dụng hệ thức lượng trong tam giác vuông OBD với đường cao BI:
\(BD^2=DI.DO\)
Áp dụng hệ thức lượng trong tam giác vuông ABD với đường cao BC:
\(BD^2=DC.DA\)
\(\Rightarrow DI.DO=DC.DA\Rightarrow\dfrac{DI}{DA}=\dfrac{DC}{DO}\)
Xét hai tam giác DCI và DOA có: \(\left\{{}\begin{matrix}\widehat{CDI}-chung\\\dfrac{DI}{DA}=\dfrac{DC}{DO}\end{matrix}\right.\)
\(\Rightarrow\Delta DCI\sim\Delta DOA\left(c.g.c\right)\) \(\Rightarrow\widehat{DCI}=\widehat{DOA}\) (1)
Do \(OM\perp AC\) tại M \(\Rightarrow M\) là trung điểm AC \(\Rightarrow AC=2CM\)
Áp dụng hệ thức lượng trong tam giác vuông ABD với đường cao BC:
\(AB^2=AC.AD\Rightarrow AB.CK=AC.AD\) (do \(AB=CK=2R\))
\(\Rightarrow\dfrac{AC}{AB}=\dfrac{CK}{AD}\Rightarrow\dfrac{2CM}{2AO}=\dfrac{CK}{AD}\Rightarrow\dfrac{CM}{AO}=\dfrac{CK}{AD}\)
Lại có \(OA=OC=R\Rightarrow\Delta OAC\) cân tại O \(\Rightarrow\widehat{OAC}=\widehat{OCA}\)
Hay \(\widehat{KCM}=\widehat{DAO}\)
Xét 2 tam giác KCM và DAO có: \(\left\{{}\begin{matrix}\dfrac{CM}{AO}=\dfrac{CK}{AD}\left(cmt\right)\\\widehat{KCM}=\widehat{DAO}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta KCM\sim\Delta DAO\left(c.g.c\right)\)
\(\Rightarrow\widehat{KMC}=\widehat{DOA}\) (2)
(1);(2) \(\Rightarrow\widehat{KMC}=\widehat{DCI}\)
\(\Rightarrow CI||MK\) (hai góc đồng vị bằng nhau) hay \(MN||CI\)
Trong tam giác ACI, đường thẳng MN song song cạnh đáy CI và đi qua trung điểm M của cạnh bên
\(\Rightarrow MN\) là đường trung bình tam giác ACI
\(\Rightarrow N\) là trung điểm AI
2.
Trong tam giác vuông ABC:
\(tan\widehat{ABC}=\dfrac{AC}{BC}=\dfrac{150}{285}=\dfrac{10}{19}\)
\(\Rightarrow\widehat{ABC}\approx27^045'\)
Hay góc hạ của tia AB xấp xỉ \(27^045'\)
Khi góc hạ bằng 46 độ ta có:
\(AC=BC.tan46^0=285.tan46^0\approx295\left(m\right)\)