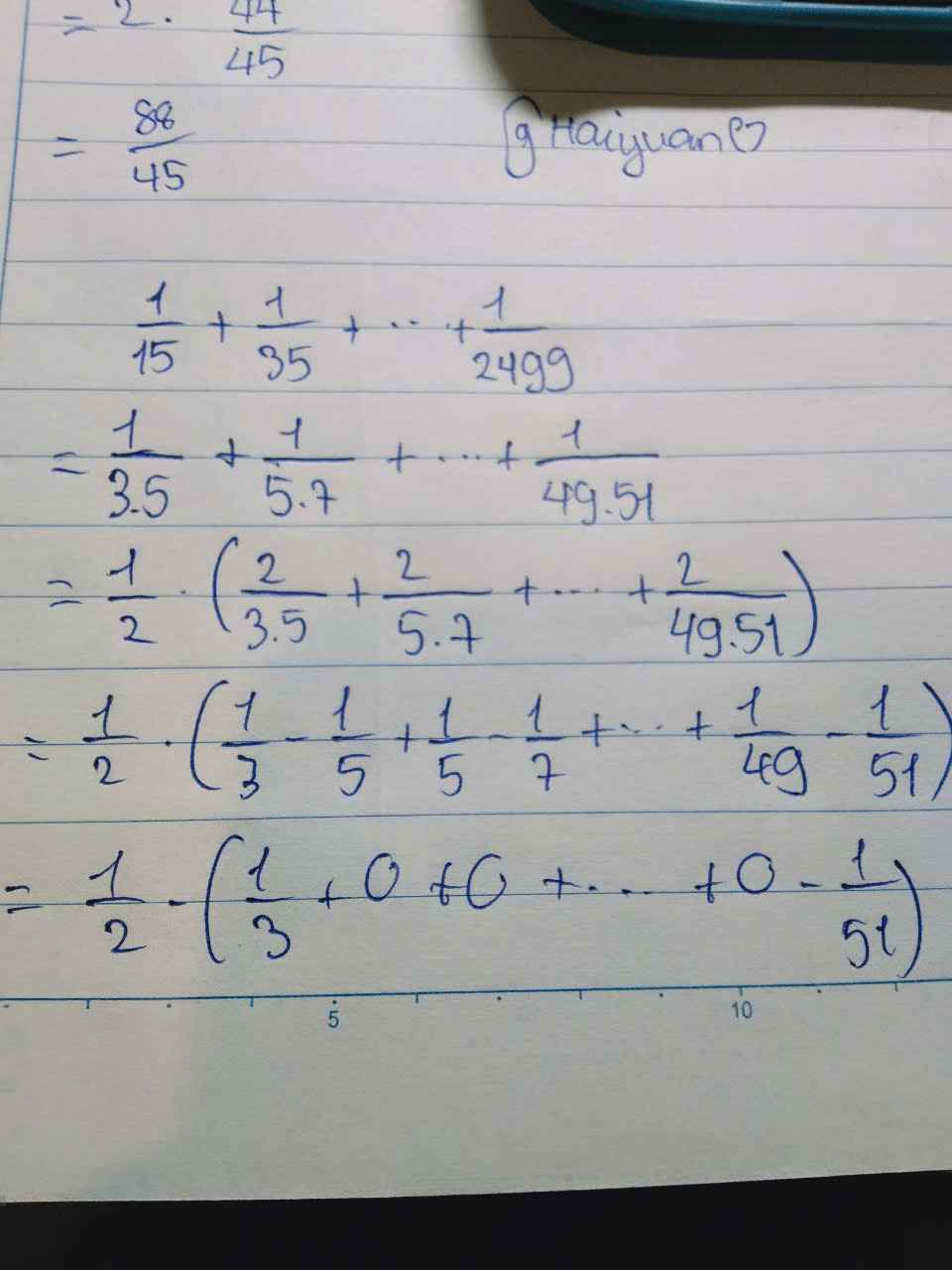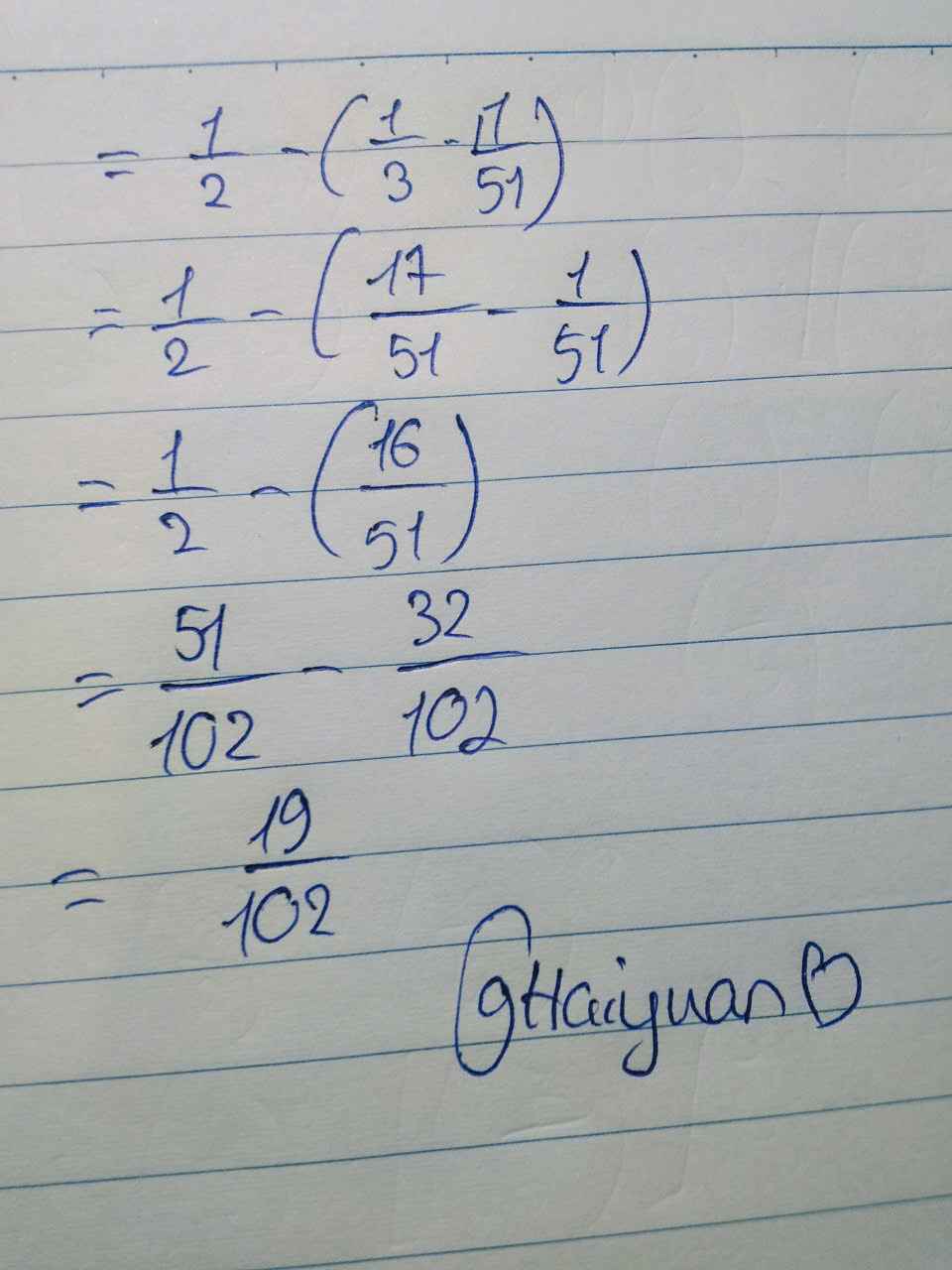\(\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{2499}\)
\(=\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{49.51}\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{49.51}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{3}-\dfrac{1}{51}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{17}{51}-\dfrac{1}{51}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{16}{51}\)
\(=1.\dfrac{8}{51}\)
`= 8/51`
`1/15 + 1/35 + ... + 1/2499`
`= 1/(3.5) + 1/(5.7) + ... + 1/(49.51)`
`= 1/2 (2/(3.5) + 2/(5.7) + ... +2/(49.51))`
`= 1/2 (1/3 - 1/5 + 1/5 - 1/7 + ... + 1/49 - 1/51)`
`= 1/2 . (1/3 - 1/51) `
`= 1/2 . 16/51`
`= 8/51`
\(\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{2499}\)
\(=\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{49.51}\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{1}{3}-\dfrac{1}{51}\right)\)
\(=\dfrac{1}{2}.\dfrac{16}{51}\)
\(=\dfrac{8}{51}\)