Các câu hỏi tương tự
cho 2 biểu thức
A=\(\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{1}{\sqrt{x}+2}-\frac{3\sqrt{x}}{x+\sqrt{x}-2}\)
B=\(\frac{\sqrt{x}+3}{\sqrt{x}+1}\)
a)Rút gọn biểu thức A
b)Tìm giá trị của x để biểu thức S=A.B có giá trị lớn nhất
Cho biểu thức\(B=2x+\frac{8}{x-3}-5\)
a>Tìm giá trị nhỏ nhất của biểu thức B.
b>Tìm giá trị của x để bểu thức B có giá trị nhỏ nhất.
Cho biểu thức
\(P=\left(\frac{1}{\sqrt{x}-1}+\frac{11}{x+\sqrt{x}+1}-\frac{34}{1-x\sqrt{x}}\right):\left(\frac{1}{\sqrt{x}-1}-\frac{\sqrt{x}+1}{x+\sqrt{x}+1}\right)\)
a)Tìm điều kiện của x để P xác định, rút gọn P?
b) tính giá trị của P khi \(x=3-2\sqrt{2}\)
c)tìm giá trị nhỏ nhất của biểu thức P? Giá trị đó đạt được khi x bằng bao nhiêu?
Cho biểu thức
A= \(\frac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\frac{2a+\sqrt{a}}{\sqrt{a}}+1\)
a, Rút gọn A
b, Tìm a để A=2
c, Tìm giá trị nhỏ nhất của A
Tìm x để các căn thức sau có nghĩa ? Bài 2: ( 3 điểm ): Rút gọn biểu thứcBài 3 (4điểm) Cho biểu thức (Với x 0; x 2; x9)a) Rút gọn biểu thức Ab) Với giá trị nào của x thì A có giá trị bằng 1/2c) Tính giá trị của A tại x 19 – 8√3d) Tìm số nguyên x để biểu thức A có giá trị là số nguyên?Bài 4(1điểm): Cho B x + 4√xTìm x để biểu thức B đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó?
Đọc tiếp
Tìm x để các căn thức sau có nghĩa ?
![]()
Bài 2: ( 3 điểm ): Rút gọn biểu thức

Bài 3 (4điểm) Cho biểu thức 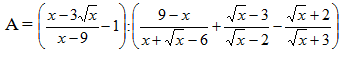
(Với x 0; x 2; x9)
a) Rút gọn biểu thức A
b) Với giá trị nào của x thì A có giá trị bằng 1/2
c) Tính giá trị của A tại x = 19 – 8√3
d) Tìm số nguyên x để biểu thức A có giá trị là số nguyên?
Bài 4(1điểm): Cho B = x + 4√x
Tìm x để biểu thức B đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó?
Cho a + b = 1. Tìm giá trị nhỏ nhất của biểu thức: M = a3 + b3.
cho biểu thức A=\(\frac{x+y-2\sqrt{xy}}{\sqrt{x}-\sqrt{y}}\)
a)tìm ĐKXĐ để A có nghĩa, rút gọn biểu thức A
b)tính giá trị của biểu thức A với x=\(9-4\sqrt{2}\) và y=\(6+4\sqrt{2}\)
bài 1: cho biểu thức: P=\(\frac{3a+\sqrt{9a}-3}{a+\sqrt{a}-2}-\frac{\sqrt{a}+1}{\sqrt{a}+2}+\frac{\sqrt{a}-2}{1-\sqrt{a}}\)
a) Rút gọn P
b) Tìm các giá trị nguyên của a để P nguyên
bài 2: cho biểu thức: P=\(\frac{\sqrt{a+4\sqrt{a-4}}+\sqrt{a-4\sqrt{a-4}}}{\sqrt{1-\frac{8}{a}+\frac{16}{a^2}}}\)
a) Rút gọn P
b) Tìm các giá trị nguyên của a (a>8) để P nguyên
\(A=\left(\frac{a\sqrt{a}-1}{a-\sqrt{a}}-\frac{a\sqrt{a}+1}{a+\sqrt{a}}\right):\frac{a+2}{a-2}\)
a) tìm đkxđ
b) rút gọ biểu thức
c) Với giá trị nguyên nào của a thì A đạt giá trị nhỏ nhất .











