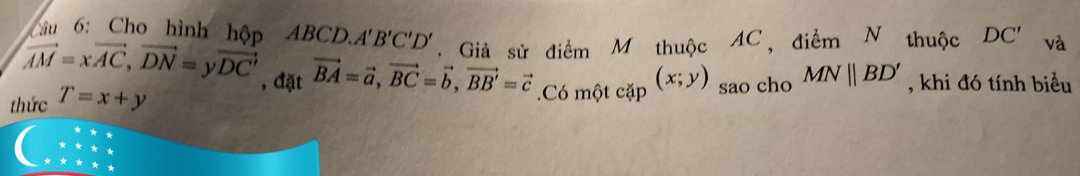\(\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DN}-\overrightarrow{AM}=\overrightarrow{BC}+y\overrightarrow{DC'}-x\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{MN}=\overrightarrow{BC}+y\left(\overrightarrow{DC}+\overrightarrow{CC'}\right)-x\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MN}=\overrightarrow{b}+y\left(\overrightarrow{c}-\overrightarrow{a}\right)-x\left(\overrightarrow{b}-\overrightarrow{a}\right)\)
\(\Rightarrow\overrightarrow{MN}=\left(x-y\right)\overrightarrow{a}+\left(1-x\right)\overrightarrow{b}+y\overrightarrow{c}\)
\(\overrightarrow{BD'}=\overrightarrow{BA}+\overrightarrow{AD'}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DD'}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)
\(\overrightarrow{MN}//\overrightarrow{BD'}\Leftrightarrow\dfrac{x-y}{1}=\dfrac{1-x}{1}=\dfrac{y}{1}=\dfrac{x-y+1-x+y}{1+1+1}=\dfrac{1}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)
\(\Rightarrow T=x+y=\dfrac{2}{3}+\dfrac{1}{3}=1\)