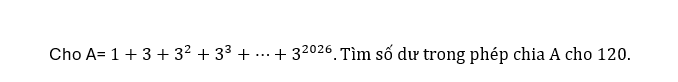Ta có: \(A=1+3+3^2+3^3+...+3^{2026}\)
\(=\left(1+3+3^2\right)+\left(3^3+3^4+3^5+3^6\right)+\left(3^7+3^8+3^9+3^{10}\right)+...+\left(3^{2023}+3^{2024}+3^{2025}+3^{2026}\right)\)
\(=13+3^2\left(3+3^2+3^3+3^4\right)+3^6\left(3+3^2+3^3+3^4\right)+...+3^{2022}\left(3+3^2+3^3+3^4\right)\)
\(=13+120\left(3^2+3^6+...+3^{2022}\right)\)
=>A chia 120 dư 13
The king and his messengers are travelling from the castle to the summer palace at a speed of 5 km/h. A long the way, the king sends a messenger back to the castle; and one hour later, he sends back another messenger. if the messenger travel at a speed of 10 km/h. What is the time between their arrivals at the castle?
(A) 30 min (B) 60 min (C) 75 min (D) 90 min (E) 120 min
Mọi người giải hộ mik bài này nhé, ở chỗ mik hok cái bài nâng cao này mak mik ko
biết làm. mong các bạn giúp!!! Cảm ơn nhiều
A=(x-5)nhân (x-3) x số nguyên A bằng giá trị nhỏ nhất
Cho P là tích của 2016 số nguyên tố đầu tiên: CMR P-1 và P+1 không phải là số chính phương
Ai giải gúp mình nha?
rút gọn phân số giúp mik với:
-8/12
15/-60
-16/-72
35/14.15
Một bể đang chứa lượng nước bằng 1/4 dung tích bể. Người ta mở một vòi nước chảy vào bể, mỗi giờ chảy được 1/8 bể. Hỏi sau bao lâu thì bể đầy nước?
Tính tổng các số nguyên x biết: a + 3 \(\le\)x\(\le\)a + 2018 ( a \(\in\)N )
So sánh N = \(\dfrac{2}{1.2}\)+\(\dfrac{2}{2.3}\)+\(\dfrac{2}{3.4}\)+...+\(\dfrac{2}{49.50}\) với 2
tìm số nguyên N để:
A=7/n-1
B=n-3/n+2
C=3n-1/2n+2
giúp mình ngay luôn được ko ạ
tìm x,y nguyên biết: 2x ( 3y - 2 ) + ( 3y - 2 ) = - 55
x/3-5/y=1/6
giải giúp mk với mình đang cần gấp
