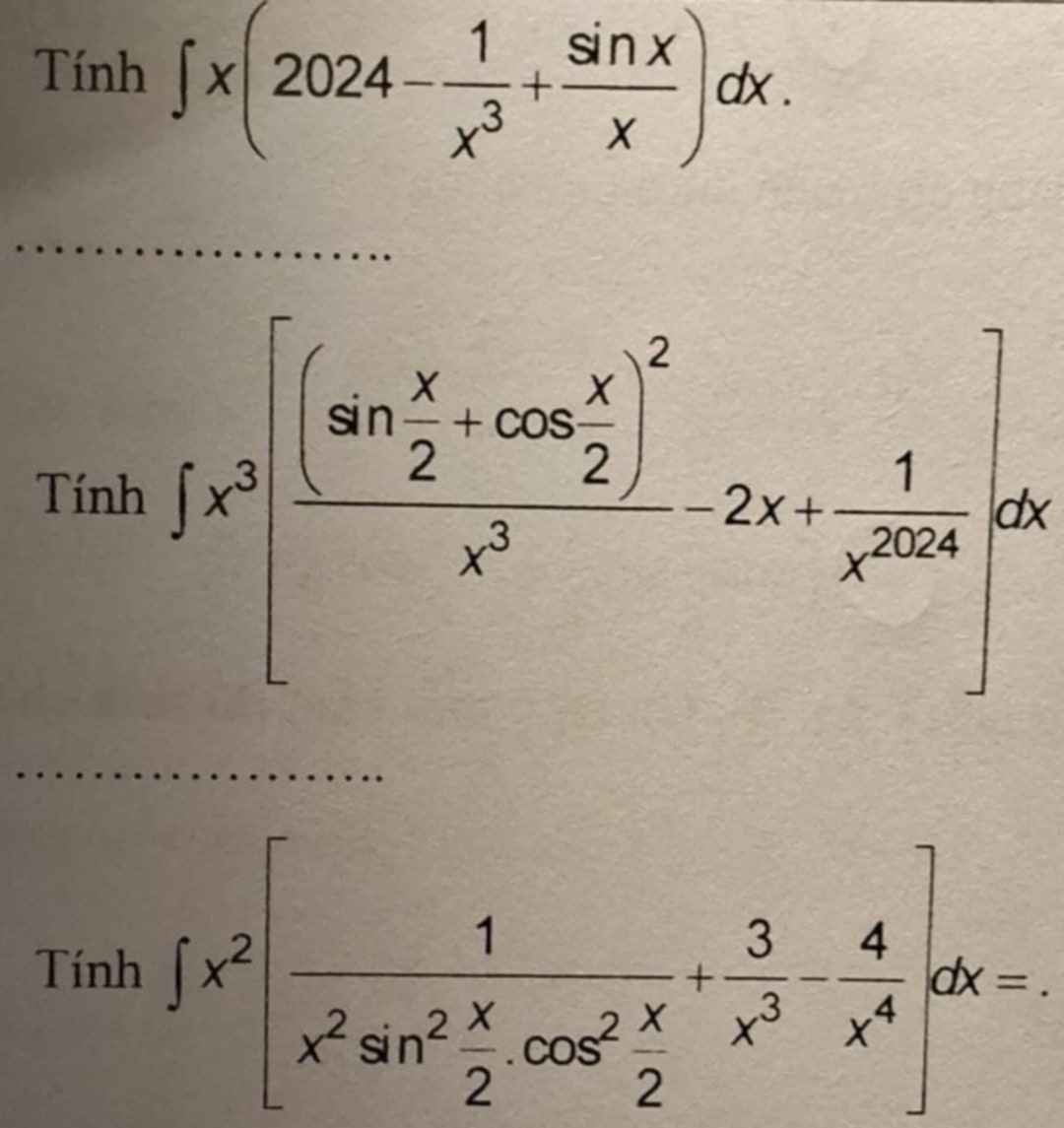c.
\(\int x^2\left[\dfrac{4}{x^2\left(2sin\dfrac{x}{2}cos\dfrac{x}{2}\right)^2}+\dfrac{3}{x^3}-\dfrac{4}{x^4}\right]dx\)
\(=\int x^2\left[\dfrac{4}{x^2.sin^2x}+\dfrac{3}{x^3}-\dfrac{4}{x^4}\right]dx\)
\(=\int\left(\dfrac{4}{sin^2x}+\dfrac{3}{x}-\dfrac{4}{x^2}\right)dx\)
\(=-4cotx+3ln\left|x\right|+\dfrac{4}{x}+C\)
a.
\(\int x\left(2024-\dfrac{1}{x^3}+\dfrac{sinx}{x}\right)dx\)
\(=\int\left(2024x-\dfrac{1}{x^2}+sinx\right)dx\)
\(=1012x^2+\dfrac{1}{x}-cosx+C\)
b.
\(\int x^3\left[\dfrac{\left(sin\dfrac{x}{2}+cos\dfrac{x}{2}\right)^2}{x^3}-2x+\dfrac{1}{x^{2024}}\right]dx\)
\(=\int\left[\left(sin\dfrac{x}{2}+cos\dfrac{x}{2}\right)^2-2x^4+\dfrac{1}{x^{2021}}\right]dx\)
\(=\int\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}+2sin\dfrac{x}{2}cos\dfrac{x}{2}-2x^4+\dfrac{1}{x^{2021}}\right)dx\)
\(=\int\left(1+sinx-2x^4+\dfrac{1}{x^{2021}}\right)dx\)
\(=x-cosx-\dfrac{2}{5}x^5-\dfrac{1}{2020.x^{2020}}+C\)