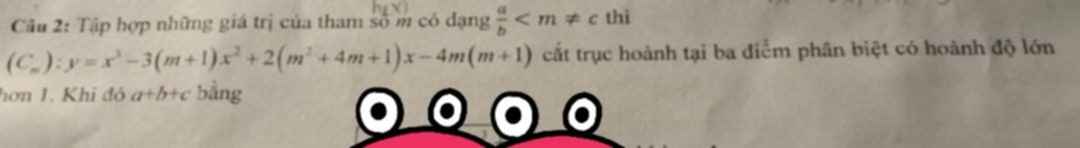\(y=x^3-3\left(m+1\right)x^2+2\left(m^2+4m+1\right)x-4m\left(m+1\right)=0\)
Bấm máy thử m = 100 ta thấy phương trình có nghiệm đẹp x = 2. Chia đa thức vế trái cho x=2 ta được
\(\Leftrightarrow\left(x-2\right)\left(x^2-\left(3m+1\right)x+2m^2+2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-\left(3m+1\right)x+2m^2+2m=0\end{matrix}\right.\)
Tính delta hoặc bấm máy thử m = 100 ta nhẩm được 2 nghiệm của phương trình dưới
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=m+1\\x=2m\end{matrix}\right.\)
Để 3 nghiệm trên là phân biệt và lớn hơn 1
\(\Rightarrow\left\{{}\begin{matrix}1< 2m\ne2\\1< m+1\ne2\\2m\ne m+1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{2}< m\ne1\\0< m\ne1\\m\ne1\end{matrix}\right.\Rightarrow}\dfrac{1}{2}< m\ne1}\)
Suy ra a=1,b=2,c=1 => a+b+c=4