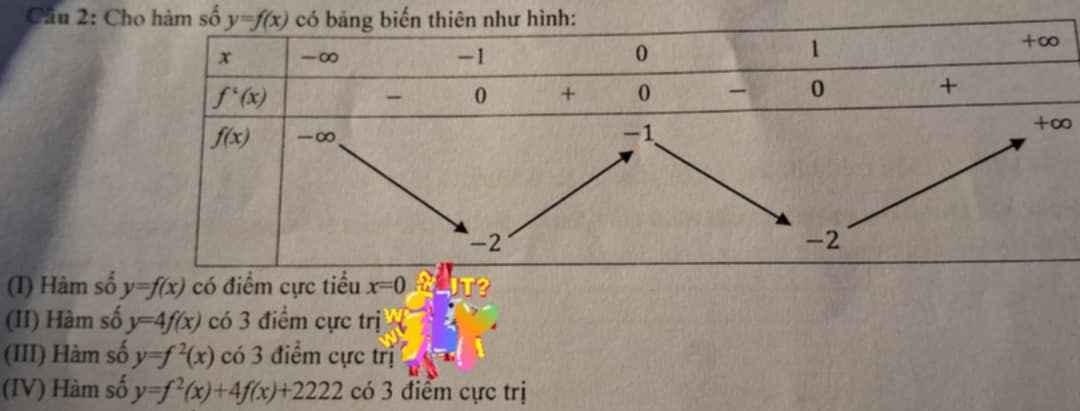
Nhìn BBT:
a. Sai (cực đại)
b. Đúng, hai hàm giống nhau về số cực trị
c. Sai
\(y'=2f\left(x\right).f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}f\left(x\right)=0\\f'\left(x\right)=0\end{matrix}\right.\)
\(f\left(x\right)=0\) có 2 nghiệm (đường thẳng `y=0` nằm cao hơn số -1 nên cắt 2 nhanh tại 2 điểm)
\(f'\left(x\right)=0\) có 3 do f(x) có 3 cực trị
Nên hàm có 5 cực trị
d. Đúng
\(y'=2f\left(x\right).f'\left(x\right)+4f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f\left(x\right)=-2\end{matrix}\right.\)
\(f'\left(x\right)=0\) có 3 nghiệm
\(y=-2\) tiếp xúc với \(f\left(x\right)\) tại 2 điểm nên ko có nghiệm đơn nào
Vậy hàm có 3 cực trị