\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)
BBT:
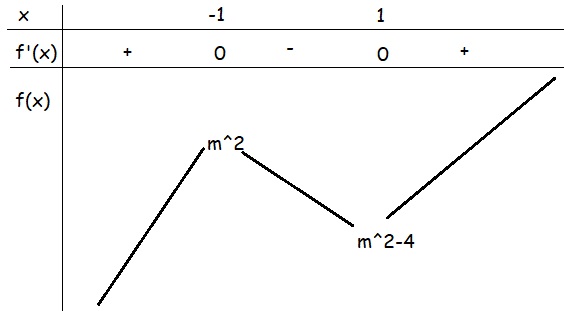
Từ BBt ta thấy:
a.
\(\max\limits_{\left[-1;1\right]}f\left(x\right)=f\left(-1\right)=m^2=0\) khi \(m=0\)
b.
Trên \(\left[-\dfrac{1}{2};\dfrac{1}{2}\right]\) hàm \(f\left(2x\right)\) nghịch biến nên \(\min\limits_{\left[-\dfrac{1}{2};\dfrac{1}{2}\right]}f\left(2x\right)=f\left(1\right)=m^2-4=-4\)
khi \(m=0\)
c.
Trên \(\left[-3;0\right]\) của hàm \(f\left(x+1\right)\) (tương đương \(\left[-2;1\right]\) của \(f\left(x\right)\)) do \(x=-1\) là cực đại và là cực trị duy nhất nên:
\(\max\limits_{\left[-3;0\right]}f\left(x+1\right)=f\left(-1\right)=m^2=1\) khi \(m=1\)
d.
\(h'\left(x\right)=-3.f'\left(1-3x\right)\)
Khi \(-2\le x\le0\Rightarrow1\le1-3x\le7\)
Trên \(\left[1;7\right]\) ta thấy \(f'\left(x\right)>0\Rightarrow f'\left(1-3x\right)>0\) trên \(\left[-2;0\right]\)
\(\Rightarrow h'\left(x\right)\le0;\forall x\in\left[-2;0\right]\Rightarrow h\left(x\right)\) nghịch biến
\(\Rightarrow\min\limits_{\left[-2;0\right]}h\left(x\right)=h\left(0\right)=f\left(1\right)=m^2-4\)
\(\Rightarrow m^2-4< 2\Rightarrow m^2< 6\Rightarrow m=\left\{-2;-1;0;1;2\right\}\)
Có 5 giá trị của m thỏa mãn










