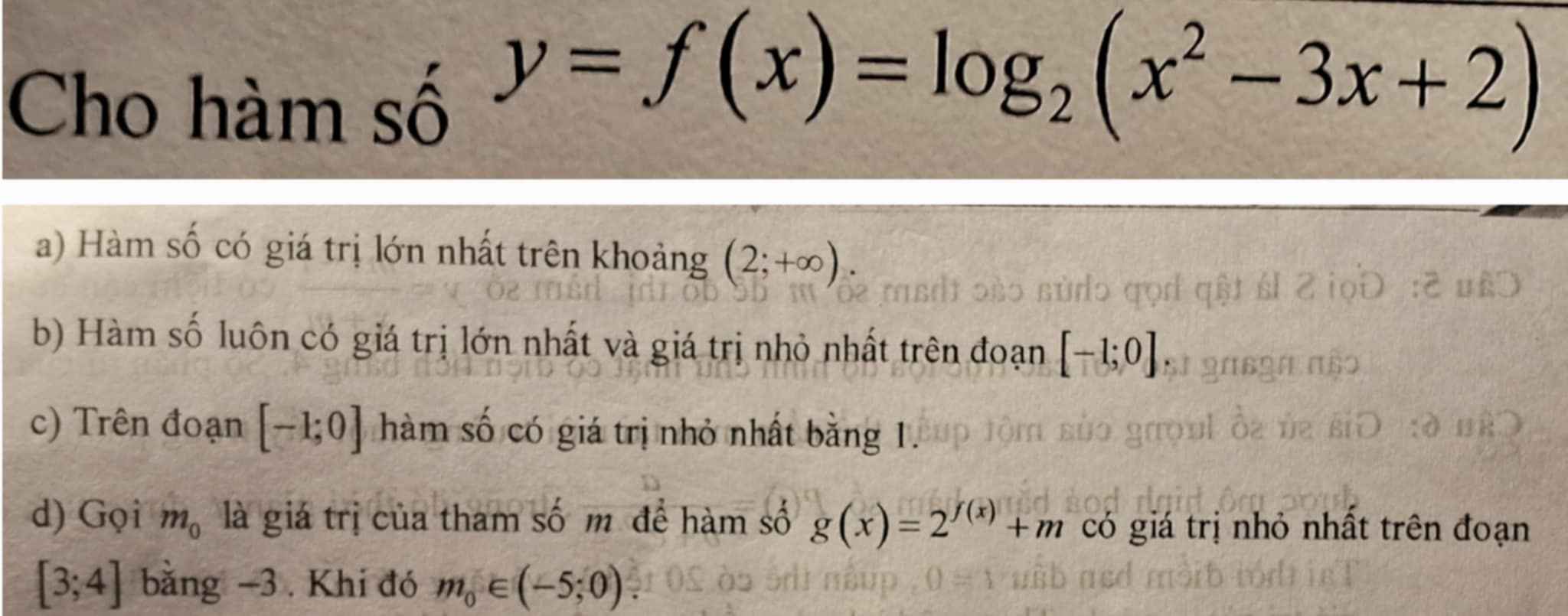ĐKXĐ: \(x^2-3x+2>0\Rightarrow\left[{}\begin{matrix}x>2\\x< 1\end{matrix}\right.\) là tập D
\(f'\left(x\right)=\dfrac{\left(2x-3\right).ln2}{x^2-3x+2}=0\Rightarrow x=\dfrac{3}{2}\notin D\) (loại)
\(\lim\limits_{x\rightarrow\pm\infty}f\left(x\right)=+\infty\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow2^+}f\left(x\right)=-\infty\)
BBT:
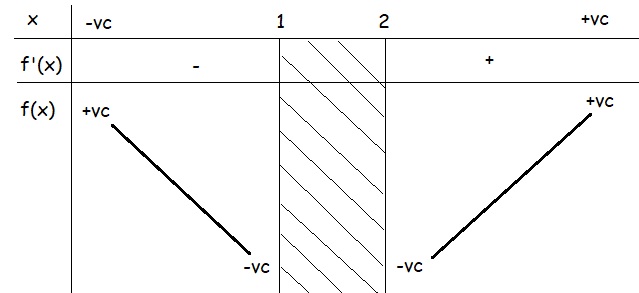
Từ BBT ta thấy:
a.
Hàm ko có GTLN trên \(\left(2;+\infty\right)\)
b.
Hàm liên tục và xác định trên \(\left[-1;0\right]\) nên có min và max trên \(\left[-1;0\right]\)
c.
Trên \(\left[-1;0\right]\subset\left(-\infty;1\right)\) hàm nghịch biến nên \(\min\limits_{\left[-1;0\right]}f\left(x\right)=f\left(0\right)=ln\left(2\right)\)
d.
\(g\left(x\right)=2^{f\left(x\right)}+m=2^{log_2\left(x^2-3x+2\right)}+m=x^2-3x+2+m\)
\(g'\left(x\right)=2x-3=0\Rightarrow x=\dfrac{3}{2}\)
\(a=1>0\Rightarrow g\left(x\right)\) đồng biến khi \(x>\dfrac{3}{2}\)
\(\Rightarrow g\left(x\right)\) đồng biến trên \(\left[3;4\right]\Rightarrow\min\limits_{\left[3;4\right]}g\left(x\right)=g\left(3\right)=m+2\)
\(\Rightarrow m+2=-3\Rightarrow m=-5\notin\left(-5;0\right)\)