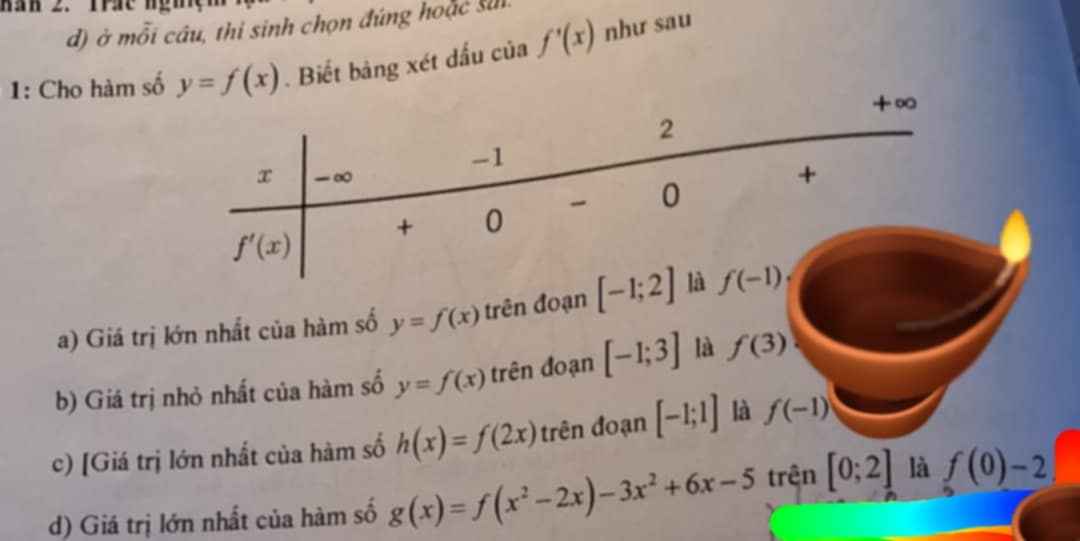a.
Trên \(\left[-1;2\right]\) hàm nghịch biến nên giá trị lớn nhất là \(f\left(-1\right)\)
b.
Trên \(\left[-1;3\right]\) hàm chỉ có 1 cực trị \(x=2\) đồng thời là cực tiểu nên giá trị nhỏ nhất là \(f\left(2\right)\)
c.
\(f\left(2x\right)\) trên \(\left[-1;1\right]\) giống \(f\left(x\right)\) trên \(\left[-2;2\right]\)
Trên \(\left[-2;2\right]\) có \(x=-1\) là cực đại duy nhất và ko có cực tiểu nên giá trị lớn nhất là \(f\left(-1\right)\)
d.
\(g'\left(x\right)=\left(2x-2\right).f'\left(x^2-2x\right)-6x+6=\left(2x-2\right).\left[f'\left(x^2-2x\right)-3\right]\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^2-2x\right)-3=0\end{matrix}\right.\)
\(x\in\left[0;2\right]\Rightarrow x^2-2x\in\left[-1;0\right]\)
Trên \(\left[-1;0\right]\) ta thấy \(f'\left(x\right)\le0\Rightarrow f'\left(x^2-2x\right)-3< 0\) vô nghiệm
\(\Rightarrow x=1\) là cực trị duy nhất đồng thời là cực đại của \(g\left(x\right)\) trên \(\left[0;2\right]\)
\(\Rightarrow\) Giá trị lớn nhất của g(x) trên \(\left[0;2\right]\) là:
\(g\left(1\right)=f\left(1^2-2.1\right)-3.1^2+6.1-5=f\left(-1\right)-2\)