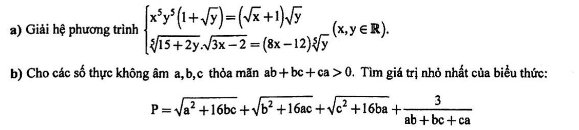Làm câu bất trước:
Ta chứng minh BĐT sau:
\(\sqrt{a^2+16bc}+\sqrt{b^2+16ca}+\sqrt{c^2+16ab}\ge6\sqrt{ab+bc+ca}\) (1)
Do vai trò a;b;c là như nhau, ko mất tính tổng quát, giả sử \(c=min\left\{a;b;c\right\}\)
Ta có: \(\sqrt{a^2+16bc}+\sqrt{b^2+16ca}\ge\sqrt{\left(a+b\right)^2+16c\left(\sqrt{a}+\sqrt{b}\right)^2}\)
Đồng thời:
\(\sqrt{c^2+16ab}\ge\sqrt{16ab}=4\sqrt{ab}\)
Nên ta chỉ cần chứng minh:
\(\sqrt{\left(a+b\right)^2+16c\left(\sqrt{a}+\sqrt{b}\right)^2}+4\sqrt{ab}\ge6\sqrt{ab+bc+ca}\)
\(\Leftrightarrow\sqrt{\left(a+b\right)^2+16c\left(\sqrt{a}+\sqrt{b}\right)^2}\ge6\sqrt{ab+bc+ca}-4\sqrt{ab}\)
Bình phương 2 vế và rút gọn:
\(\Leftrightarrow\left(a+b\right)^2+32c\sqrt{ab}+48\sqrt{ab\left(ab+bc+ca\right)}\ge20\left(ac+bc\right)+52ab\)
Do \(c=min\left\{a;b;c\right\}\Rightarrow2ab\ge bc+ca\)
\(\Rightarrow3ab\ge bc+bc\Rightarrow3ab\left(bc+ca\right)\ge\left(bc+ca\right)^2\)
Nên: \(ab\left(ab+bc+ca\right)=\dfrac{9\left(ab\right)^2+6ab\left(bc+ca\right)+3ab\left(bc+ca\right)}{9}\)
\(\ge\dfrac{9\left(ab\right)^2+6ab\left(bc+ca\right)+\left(bc+ca\right)^2}{9}=\left(\dfrac{3ab+bc+ca}{3}\right)^2\)
\(\Rightarrow48\sqrt{ab\left(ab+bc+ca\right)}\ge48\left(\dfrac{3ab+bc+ca}{3}\right)=48ab+16\left(bc+ca\right)\)
Do đó ta cần chứng minh:
\(\left(a+b\right)^2+32c\sqrt{ab}\ge4ab+4c\left(a+b\right)\)
\(\Leftrightarrow\left(a+b\right)^2+32c\sqrt{ab}-4c\left(a+b\right)-4ab\ge0\)
Do \(c=min\left\{a;b;c\right\}\Rightarrow c\le\sqrt{ab}\Rightarrow0\le c\le\sqrt{ab}\)
Hàm \(f\left(c\right)=\left(a+b\right)^2+32c\sqrt{ab}-4c\left(a+b\right)-4ab\) là hàm bậc nhất theo c nên đơn điệu trên R
\(\Rightarrow\min\limits_{c\in\left[0;\sqrt{ab}\right]}f\left(c\right)=min\left\{f\left(0\right);f\left(\sqrt{ab}\right)\right\}\)
\(f\left(0\right)=\left(a+b\right)^2-4ab=\left(a-b\right)^2\ge0\)
\(f\left(\sqrt{ab}\right)=\left(a+b\right)^2+28ab-4\left(a+b\right)\sqrt{ab}\ge2\sqrt{\left(a+b\right)^2.28ab}-4\left(a+b\right)\sqrt{ab}\)
\(\Rightarrow f\left(\sqrt{ab}\right)\ge4\left(a+b\right)\sqrt{ab}\left(\sqrt{7}-1\right)\ge0\)
\(\Rightarrow min\left\{f\left(0\right);f\left(\sqrt{ab}\right)\right\}\ge0\)
\(\Rightarrow f\left(c\right)\ge0;\forall a;b;c\) (đpcm)
Do đó:
\(P\ge3\sqrt{ab+bc+ca}+3\sqrt{ab+bc+ca}+\dfrac{3}{ab+bc+ca}\ge3.3\sqrt[3]{\dfrac{ab+bc+ca}{ab+bc+ca}}=9\)
\(P_{min}=9\) khi \(\left(a;b;c\right)=\left(1;1;0\right)\) và các hoán vị
Câu hệ (cách giải ko tối ưu, nhưng ko nghĩ ra cách nào tốt hơn)
\(y=0\Rightarrow x=\dfrac{2}{3}\) là 1 nghiệm
Với \(y>0\Rightarrow x>\dfrac{3}{2}\)
Biến đổi pt đầu:
\(a^{10}.b^{10}\left(1+b\right)=\left(a+1\right)b\)
\(\Leftrightarrow b^9\left(1+b\right)=\dfrac{a+1}{a^{10}}\)
\(\Leftrightarrow b^9+b^{10}=\left(\dfrac{1}{a}\right)^9+\left(\dfrac{1}{a}\right)^{10}\)
Hàm \(f\left(t\right)=t^9+t^{10}\) hiển nhiên đồng biến khi \(t>0\)
\(\Rightarrow b=\dfrac{1}{a}\Rightarrow y=\dfrac{1}{x}\)
Thế vào pt dưới:
\(\Leftrightarrow\dfrac{8x-12}{\sqrt{3x-2}}-\sqrt[5]{15x+2}=0\)
Nhận thấy \(x=2\) là 1 nghiệm
Xét hàm \(f\left(x\right)=\dfrac{8x-12}{\sqrt{3x-2}}-\sqrt[5]{15x+2}\) khi \(x>\dfrac{3}{2}\)
\(f'\left(x\right)=\dfrac{12x+2}{\left(3x-2\right)\sqrt{3x-2}}-\dfrac{3}{\sqrt[5]{\left(15x+2\right)^4}}\)
Do \(x>0\Rightarrow15x+2>1\Rightarrow\sqrt[5]{\left(15x+4\right)^4}>\sqrt[8]{\left(15x+2\right)^4}=\sqrt{15x+2}>\sqrt{3x-2}\)
\(\Rightarrow f'\left(x\right)>\dfrac{12x+2}{\left(3x-2\right)\sqrt{3x-2}}-\dfrac{3}{\sqrt{3x-2}}=\dfrac{3x+8}{\left(3x-2\right)\sqrt{3x-2}}>0;\forall x>\dfrac{3}{2}\)
\(\Rightarrow f\left(x\right)\) đồng biến khi \(x>\dfrac{3}{2}\)
\(\Rightarrow f\left(x\right)=0\) có đúng 1 nghiệm \(x=2\)