Câu 24 : Sửa lại đề \(I\left(\dfrac{1}{2};-\dfrac{1}{2}\right)\) vì \(y_I=-\dfrac{1}{2}\ne\dfrac{7}{4}\) không đúng với \(y=\dfrac{-2x^2+bx+c}{4x+n}\)
\(x_I=-\dfrac{n}{4}=\dfrac{1}{2}\Rightarrow n=2\)
\(\left(0;1\right)\in y\Leftrightarrow\dfrac{c}{n}=1\Leftrightarrow c=n=-2\)
Tiệm cận xiên \(y=-\dfrac{1}{2}x+\dfrac{b-1}{4}\) qua \(I\left(\dfrac{1}{2};-\dfrac{1}{2}\right)\)
\(\Rightarrow-\dfrac{1}{2}.\dfrac{1}{2}+\dfrac{1}{4}\left(b-1\right)=\dfrac{1}{2}\Leftrightarrow b-2=2\Leftrightarrow b=4\)
\(T=b^2+c^2-n=16+4+2=22\)
Nên xem lại đáp án
Câu 25 :
\(TCN:x=1\Rightarrow x+c=x-1\Rightarrow c=-1\)
\(TCX:y=ax+b\)
\(\left(0;1\right)\in TCX\Leftrightarrow b=1\Rightarrow TCX:y=ax+1\)
\(\left(1;2\right)\in TCX\Leftrightarrow a+1=2\Leftrightarrow a=1\)
\(\Rightarrow a+b+c=1\Rightarrow Chọn.A\)
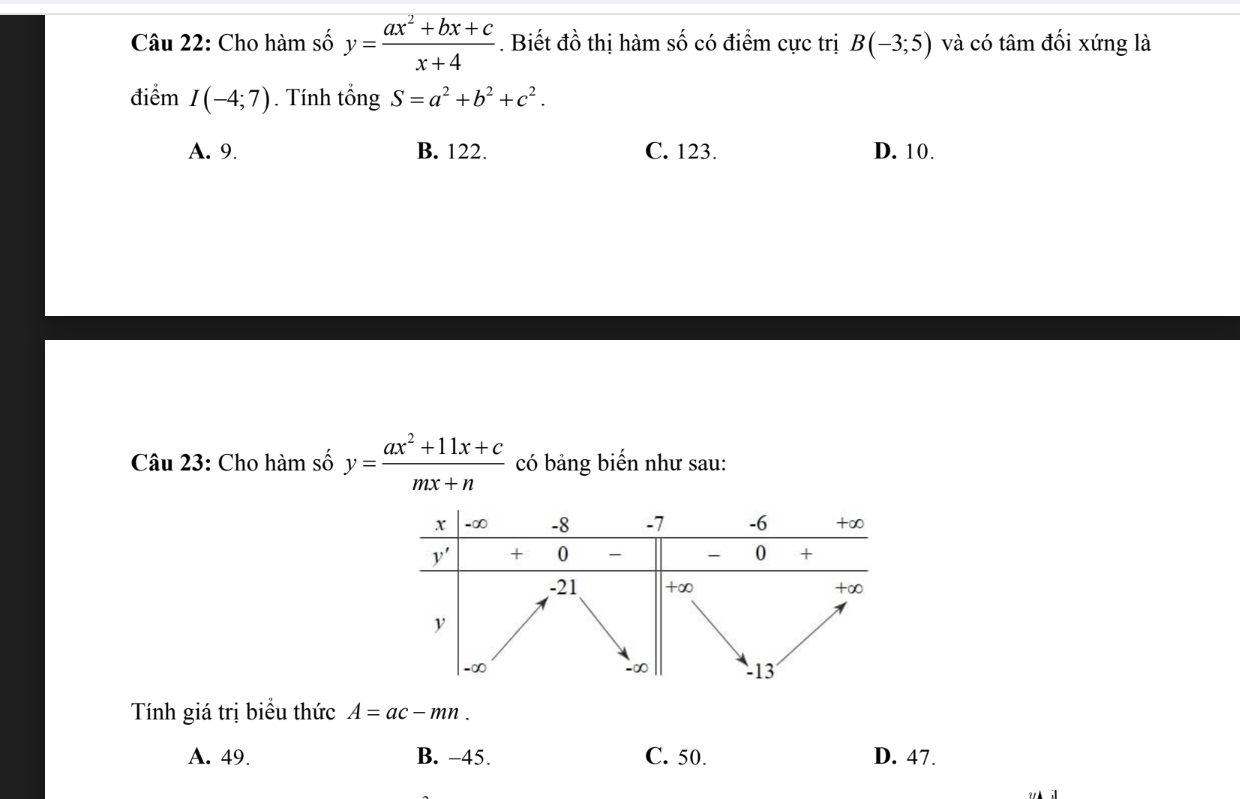
Câu 22 :
\(y_I=a=7\Rightarrow a=7\Rightarrow y=\dfrac{7x^2+bx+c}{x+4}\left(C\right)\)
Phương trình đường thẳng qua 2 điểm cực trị \(y=2ax+b=14x+b\left(d\right)\)
\(B\left(-3;5\right)\in\left(d\right)\Leftrightarrow-42+b=5\Leftrightarrow b=47\)
\(\Rightarrow\left(d\right):y=14x+47\)
\(B\left(-3;5\right)\in\left(C\right)\Leftrightarrow\dfrac{7.9+47.\left(-3\right)+c}{-3+4}=5\Leftrightarrow-78+c=5\Leftrightarrow c=83\)
\(S=a^2+b^2+c^2=49+2209+6889=9147\)
Nên xem lại đáp án
24.
Hoành độ tâm đối xứng là tiệm cận đứng nên:
\(\dfrac{1}{2}=-\dfrac{n}{4}\Rightarrow n=-2\)
Thay \(x=0\) vào pt hàm số ta được giao của đồ thị và trục tung nên:
\(\dfrac{c}{n}=1\Rightarrow c=n=-2\)
Tiệm cận xiên của đồ thị \(y=\dfrac{ax^2+bx+c}{mn+n}\) có pt: \(y=\dfrac{a}{m}x+\dfrac{bm-an}{m^2}\)
Thay vào bài: \(y=-\dfrac{1}{2}x+\dfrac{4b-4}{16}=-\dfrac{1}{2}x+\dfrac{b-1}{4}\) (1)
Tiệm cận xiên đi qua tâm đối xứng nên thay tọa độ tâm đối xứng vào (1) được:
\(-\dfrac{1}{2}.\dfrac{1}{2}+\dfrac{b-1}{4}=\dfrac{7}{4}\Rightarrow b=9\)
Đáp án A đúng
25.
Từ đồ thị thấy tiệm cận xiên đi qua 2 điểm (0;1) và (1;2) nên có pt \(y=x+1\)
\(\Rightarrow a=b=1\)
\(x=1\) là tiệm cận đứng nên \(-c=1\Rightarrow c=-1\)
A đúng
22.
Thay tọa độ B vào pt hàm số được: \(9a-3b+c=5\) (1)
Pt tiệm cận xiên có dạng: \(y=\dfrac{a}{1}x+\dfrac{b.1-4a}{1^2}=ax-4a+b\)
Tâm đối xứng thuộc tiệm cận xiên nên: \(-8a+b=7\) (2)
\(y'=\dfrac{\left(2ax+b\right)\left(x+4\right)-\left(ax^2+bx+c\right)}{\left(x+4\right)^2}=\dfrac{ax^2+8ax+4b-c}{\left(x+4\right)^2}\)
\(x=-3\Rightarrow y'=0\) nên \(9a-12a+4b-c=0\Leftrightarrow-3a+4b-c=0\) (3)
(1);(2);(3) có hệ: \(\left\{{}\begin{matrix}9a-3b+c=5\\-8a+b=7\\-15a+4b-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=-1\\c=11\end{matrix}\right.\)
C đúng
23.
2 điểm cực trị có tọa độ (-8;-21) và (-6;-13) nên pt đường thẳng qua 2 cực trị có dạng: \(y=4x+11\) (1)
Mặt khác ta có pt đường thẳng qua 2 cực trị của đồ thị \(y=\dfrac{ax^2+bx+c}{mx+n}\) là \(y=\dfrac{2a}{m}x+\dfrac{b}{m}=\dfrac{2a}{m}x+\dfrac{11}{m}\) (2)
(1);(2) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{2a}{m}=4\\\dfrac{11}{m}=11\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=1\\a=2\end{matrix}\right.\)
Tiệm cận đứng: \(x=-\dfrac{n}{m}=-7\Rightarrow n=7m=7\)
\(\Rightarrow y=\dfrac{2x^2+11x+c}{x+7}\)
Thay tọa độ \(\left(-8;-21\right)\) vào pt hàm số ta được:
\(\dfrac{2.\left(-8\right)^2+11.\left(-8\right)+c}{-8+1}=-21\Rightarrow c=-19\)
B đúng