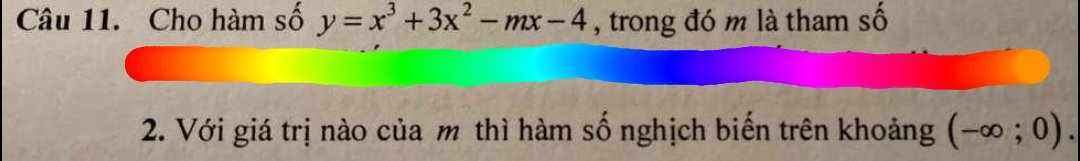\(y'=3x^2+6x-m\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\) khi và chỉ khi:
\(y'\le0;\forall x< 0\)
\(\Rightarrow3x^2+6x-m\le0;\forall x< 0\)
\(\Rightarrow m\ge\max\limits_{x< 0}\left(3x^2+6x\right)\)
Mà ko tồn tại \(\max\limits_{x< 0}\left(3x^2+6x\right)\) nên ko tồn tại m thỏa mãn yêu cầu.
Trong trắc nghiệm thì có thể nhớ quy tắc thế này:
Cho hàm số bậc 3 \(y=ax^3+bx^2+cx+d\)
- Nếu \(a>0\) thì hàm luôn đồng biến trên các khoảng chứa vô cực (cả âm vô cực lẫn dương vô cực)
- Nếu \(a< 0\) thì hàm luôn nghịch biến trên các khoảng chứa vô cực (cả âm vô cực lẫn dương vô cực)
Nhìn vào quy tắc trên thấy ngay ko tồn tại m
Đúng 3
Bình luận (0)
