Question

Answer 1

1: \(y'=-3x^2+6x\)

Để hàm số đồng biến thì y'>0

=>\(-3x^2+6x>0\)

=>-3x(x-2)>0

=>x(x-2)<0

=>0<x<2

Để hàm số nghịch biến thì y'<0

=>x(x-2)>0

=>\(\left[{}\begin{matrix}x>2\\x< 0\end{matrix}\right.\)

Vẽ đồ thị: 

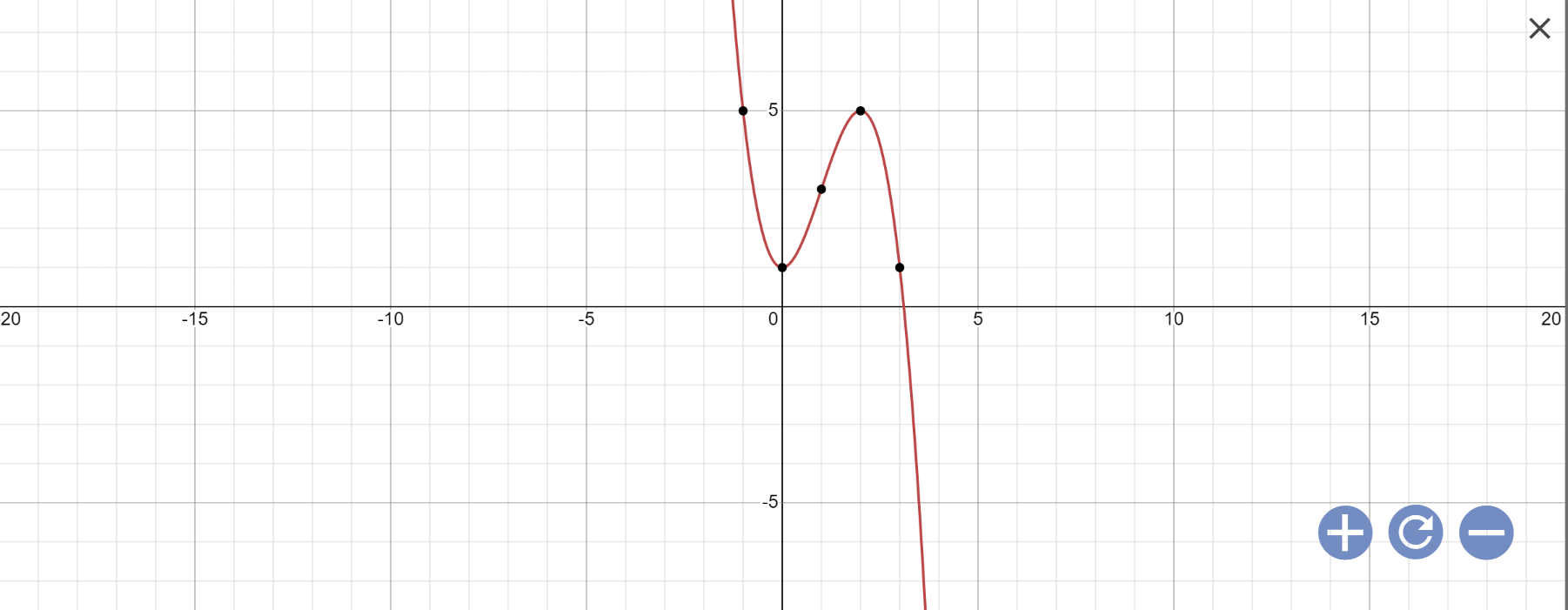
2: \(y=-x^3+3x^2+1\)

=>\(y'=-3x^2+3\cdot2x=-3x^2+6x\)

\(y'\left(3\right)=-3\cdot3^2+6\cdot3=-27+18=-9\)

Phương trình tiếp tuyến của (C) tại A(3;1) có dạng là:

\(y-y\left(3\right)=y'\left(3\right)\left(x-3\right)\)

=>\(y-1=-9\left(x-3\right)=-9x+27\)

=>y=-9x+28