Đơn giản thế này:
\(u=\left|x^2-3x+2\right|+2m\)
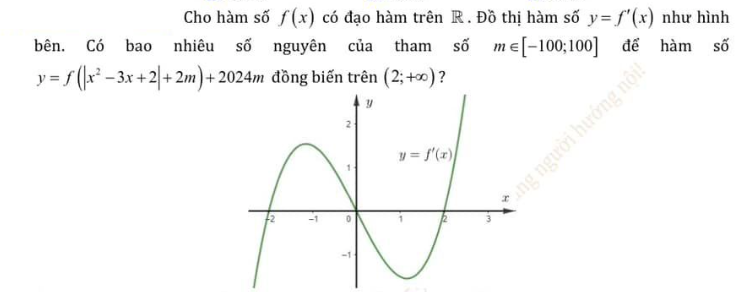
Để ý cái đầu tiên: hàm \(f\left(x\right)\) và hàm u thì ngoài cùng bên phải đều tăng lên dương vô cùng, nên ta chỉ cần quan tâm duy nhất đoạn cuối của cực trị (nghĩa là \(y=f\left(u\right)\) có các cực trị \(x_1< x_2< ...< x_n\) thì nó luôn đồng biến trên \(\left(x_n;+\infty\right)\Rightarrow\) đây là thứ ta quan tâm: nghiệm lớn nhất của \(f'\left(u\right)\), để thỏa mãn thì \(\left(2;+\infty\right)\subset\left(x_n;+\infty\right)\Rightarrow x_n\le2\)
BBT u:
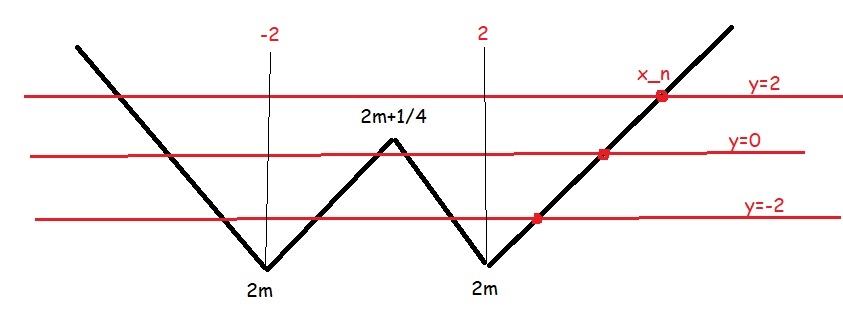
Nhìn BBT thấy ngay:
Nếu ít nhất 1 trong 3 đường thẳng \(y=-2;0;2\) cắt đồ thị u \(\Rightarrow x_n>2\) (ktm)
Do đó bài toán chỉ thỏa mãn khi đường \(y=2\) tiếp xúc hoặc thấp hơn đồ thị u
\(\Rightarrow2m\ge2\Rightarrow m\ge1\)