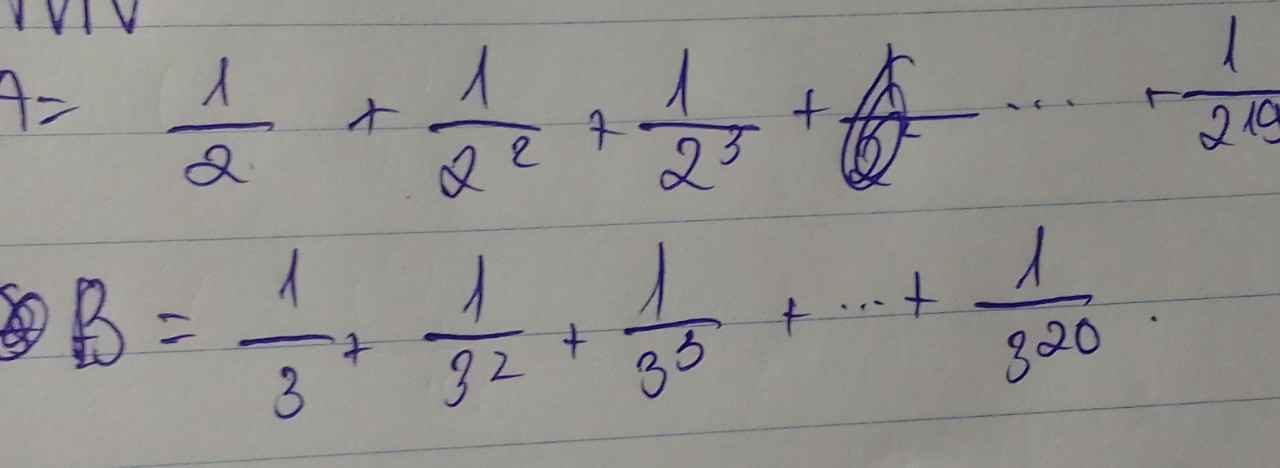A= \(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{19}}\)
2A= \(\dfrac{2}{2}+\dfrac{2}{2^2}+\dfrac{2}{2^3}+...+\dfrac{2}{2^{19}}\)
2A= \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{18}}\)
2A-A=\(\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{18}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{19}}\right)\)
A= \(1-\dfrac{1}{2^{19}}\)
B= \(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{20}}\)
3B= \(\dfrac{3}{3}+\dfrac{3}{3^2}+\dfrac{3}{3^3}+...+\dfrac{3}{3^{20}}\)
3B= \(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}\)
3B-B= \(\left(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{20}}\right)\)
2B= \(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{19}}-\dfrac{1}{3}-\dfrac{1}{3^2}-\dfrac{1}{3^3}-...-\dfrac{1}{3^{20}}\)
2B=\(1-\dfrac{1}{3^{20}}\)
A=1/2+1/22+1/23+. . .+1/219
2A=1+1/2+1/22+. . .+1/218
2A-A=(1+1/2+1/22+. . .+1/218)-(1/2+1/22+1/23+. . . +1/219)
A=1-1/219