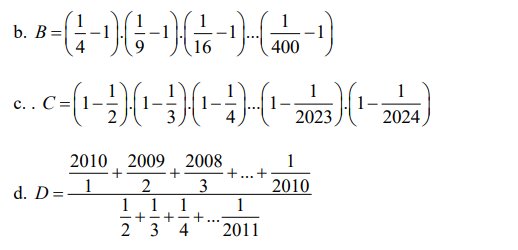b: \(B=\left(\dfrac{1}{4}-1\right)\cdot\left(\dfrac{1}{9}-1\right)\cdot...\cdot\left(\dfrac{1}{400}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{20}-1\right)\cdot\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{20}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-19}{20}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{21}{20}\)
\(=\dfrac{1}{20}\cdot\dfrac{21}{2}=\dfrac{21}{40}\)
c: \(C=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)\cdot...\cdot\left(1-\dfrac{1}{2024}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2023}{2024}\)
\(=\dfrac{1}{2024}\)
d: \(D=\dfrac{\dfrac{2010}{1}+\dfrac{2009}{2}+\dfrac{2008}{3}+...+\dfrac{1}{2010}}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2011}}\)
\(=\dfrac{\left(1+\dfrac{2009}{2}\right)+\left(1+\dfrac{2008}{3}\right)+...+\left(1+\dfrac{1}{2010}\right)+1}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2011}}\)
\(=\dfrac{\dfrac{2011}{2}+\dfrac{2011}{3}+...+\dfrac{2011}{2010}+\dfrac{2011}{2011}}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2011}}=\dfrac{2011\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2011}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2011}}\)
=2011