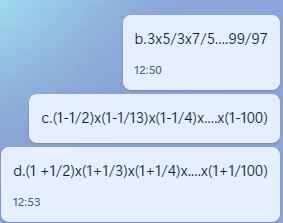
\(b.3\times\dfrac{5}{3}\times\dfrac{7}{5}\times...\times\dfrac{99}{97}\\ =\dfrac{3\times5\times7\times...\times99}{3\times5\times...\times97}\\ =\dfrac{\left(3\times5\times7\times...\times97\right)\times99}{3\times5\times7\times...\times97}\\ =99\\ c.\left(1-\dfrac{1}{2}\right)\times\left(1-\dfrac{1}{3}\right)\times\left(1-\dfrac{1}{4}\right)\times...\times\left(1-\dfrac{1}{100}\right)\\ =\dfrac{1}{2}\times\dfrac{2}{3}\times\dfrac{3}{4}\times...\times\dfrac{99}{100}\\ =\dfrac{1\times2\times3\times...\times99}{2\times3\times4\times...\times100}\\ =\dfrac{2\times3\times4\times...\times99}{\left(2\times3\times4\times...\times99\right)\times100}\\ =\dfrac{1}{100}\\ d.\left(1+\dfrac{1}{2}\right)\times\left(1+\dfrac{1}{3}\right)\times\left(1+\dfrac{1}{4}\right)\times...\times\left(1+\dfrac{1}{100}\right)\\ =\dfrac{3}{2}\times\dfrac{4}{3}\times\dfrac{5}{4}\times..\times\dfrac{101}{100}\\ =\dfrac{3\times4\times5\times...\times101}{2\times3\times4\times...\times100}\\ =\dfrac{\left(3\times4\times5\times...\times100\right)\times101}{\left(3\times4\times5\times...\times100\right)\times2}\\ =\dfrac{101}{2}\)
