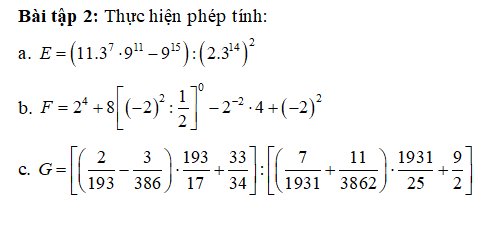\(a)E=\left(11\cdot3^7\cdot9^{11}-9^{15}\right):\left(2\cdot3^{14}\right)^2\\ =\left[11\cdot3^7\cdot\left(3^2\right)^{11}-\left(3^2\right)^{15}\right]:\left(2\cdot3^{14}\right)^2\\ =\left(11\cdot3^7\cdot3^{22}-3^{30}\right):\left[2^2\cdot\left(3^{14}\right)^2\right]\\ =\left(11\cdot3^{29}-3^{30}\right):\left(2^2\cdot3^{28}\right)\\ =3^{29}\cdot\left(11-3\right):\left(4\cdot3^{28}\right)\\ =\dfrac{3^{29}\cdot8}{3^{28}\cdot4}\\ =3\cdot2\\ =6\\ b)F=2^4+8\left[\left(-2\right)^2:\dfrac{1}{2}\right]^0-2^{-2}\cdot4+\left(-2\right)^2\\ =2^4+8\cdot1-\dfrac{1}{2^2}\cdot2^2+4\\ =16+8-1+4\\ =27\)
\(G=\left[\left(\dfrac{2}{193}-\dfrac{3}{386}\right)\cdot\dfrac{193}{17}+\dfrac{33}{34}\right]:\left[\left(\dfrac{7}{1931}+\dfrac{11}{3862}\right)\cdot\dfrac{1931}{25}+\dfrac{9}{2}\right]\\ =\left[\left(\dfrac{4}{386}-\dfrac{3}{386}\right)\cdot\dfrac{193}{17}+\dfrac{33}{34}\right]:\left[\left(\dfrac{14}{3862}+\dfrac{11}{3862}\right)\cdot\dfrac{1931}{25}+\dfrac{9}{2}\right]\\ =\left(\dfrac{1}{386}\cdot\dfrac{193}{17}+\dfrac{33}{34}\right):\left(\dfrac{25}{3862}\cdot\dfrac{1931}{25}+\dfrac{9}{2}\right)\\ =\left(\dfrac{1}{34}+\dfrac{33}{34}\right):\left(\dfrac{1}{2}+\dfrac{9}{2}\right)\\ =\dfrac{34}{34}:\dfrac{10}{2}\\ =1:5=\dfrac{1}{5}\)