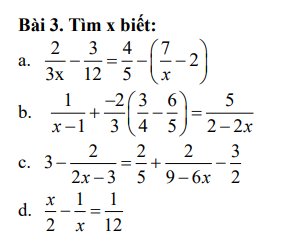a:
ĐKXĐ: x<>0
\(\dfrac{2}{3x}-\dfrac{3}{12}=\dfrac{4}{5}-\left(\dfrac{7}{x}-2\right)\)
=>\(\dfrac{2}{3x}-\dfrac{1}{4}=\dfrac{4}{5}-\dfrac{7}{x}+2=\dfrac{14}{5}-\dfrac{7}{x}\)
=>\(\dfrac{2}{3x}+\dfrac{7}{x}=\dfrac{14}{5}+\dfrac{1}{4}\)
=>\(\dfrac{2}{3x}+\dfrac{21}{3x}=\dfrac{56}{20}+\dfrac{5}{20}\)
=>\(\dfrac{23}{3x}=\dfrac{61}{20}\)
=>\(3x=20\cdot\dfrac{23}{61}=\dfrac{460}{61}\)
=>\(x=\dfrac{460}{61\cdot3}=\dfrac{460}{183}\)(nhận)
b:
ĐKXĐ: \(x\ne1\)
\(\dfrac{1}{x-1}+\dfrac{-2}{3}\left(\dfrac{3}{4}-\dfrac{6}{5}\right)=\dfrac{5}{2-2x}\)
=>\(\dfrac{1}{x-1}+\dfrac{-2}{3}\cdot\dfrac{15-24}{20}=\dfrac{-5}{2\left(x-1\right)}\)
=>\(\dfrac{1}{x-1}+\dfrac{5}{2\left(x-1\right)}+\dfrac{-2}{3}\cdot\dfrac{-9}{20}=0\)
=>\(\dfrac{7}{2\left(x-1\right)}+\dfrac{18}{60}=0\)
=>\(\dfrac{7}{2\left(x-1\right)}=\dfrac{-3}{10}\)
=>\(2\left(x-1\right)=7\cdot\dfrac{10}{-3}=\dfrac{-70}{3}\)
=>\(x-1=-\dfrac{70}{3}:2=-\dfrac{35}{3}\)
=>\(x=-\dfrac{35}{3}+1=-\dfrac{32}{3}\)
c: ĐKXĐ:x<>3/2
\(3-\dfrac{2}{2x-3}=\dfrac{2}{5}+\dfrac{2}{9-6x}-\dfrac{3}{2}\)
=>\(3-\dfrac{2}{2x-3}=\dfrac{-11}{10}-\dfrac{2}{3\left(2x-3\right)}\)
=>\(\dfrac{-2}{2x-3}+\dfrac{2}{3\left(2x-3\right)}=\dfrac{-11}{10}-3\)
=>\(\dfrac{-4}{3\left(2x-3\right)}=\dfrac{-41}{10}\)
=>\(3\left(2x-3\right)=\dfrac{-4\cdot10}{-41}=\dfrac{40}{41}\)
=>\(2x-3=\dfrac{40}{41}:3=\dfrac{40}{123}\)
=>\(2x=\dfrac{40}{123}+3=\dfrac{409}{123}\)
=>\(x=\dfrac{409}{123}:2=\dfrac{409}{246}\left(nhận\right)\)
d: ĐKXĐ: x<>0
\(\dfrac{x}{2}-\dfrac{1}{x}=\dfrac{1}{12}\)
=>\(\dfrac{x^2-2}{2x}=\dfrac{1}{12}\)
=>\(12\left(x^2-2\right)=2x\)
=>\(6\left(x^2-2\right)=x\)
=>\(6x^2-x-12=0\)
=>\(6x^2-9x+8x-12=0\)
=>3x(2x-3)+4(2x-3)=0
=>(2x-3)(3x+4)=0
=>\(\left[{}\begin{matrix}x=\dfrac{3}{2}\left(nhận\right)\\x=-\dfrac{4}{3}\left(nhận\right)\end{matrix}\right.\)