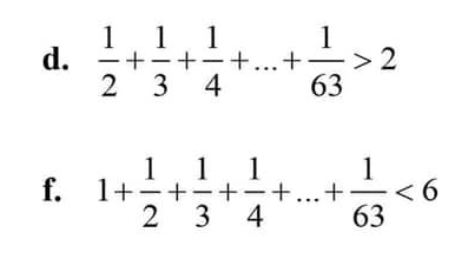
d. Ta có: \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{63}\)
\(=\dfrac{1}{2}+\left(\dfrac{1}{3}+\dfrac{1}{4}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}\right)+...+\left(\dfrac{1}{33}+\dfrac{1}{34}+\dfrac{1}{35}+...+\dfrac{1}{63}+\dfrac{1}{64}\right)-\dfrac{1}{64}\)
\(>\dfrac{1}{2}+2\cdot\dfrac{1}{4}+4\cdot\dfrac{1}{8}+...+32\cdot\dfrac{1}{64}-\dfrac{1}{64}\)
\(=\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+...+\dfrac{1}{2}-\dfrac{1}{64}\)
\(=3-\dfrac{1}{64}>2\) (đpcm)
f. Lại có: \(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{63}\)
\(=1+\left(\dfrac{1}{2}+\dfrac{1}{3}\right)+\left(\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}\right)+\left(\dfrac{1}{8}+\dfrac{1}{9}+...+\dfrac{1}{15}\right)+\left(\dfrac{1}{16}+\dfrac{1}{17}+...+\dfrac{1}{31}\right)+\left(\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{63}\right)\)
\(< 1+2\cdot\dfrac{1}{2}+4\cdot\dfrac{1}{4}+8\cdot\dfrac{1}{8}+16\cdot\dfrac{1}{16}+32\cdot\dfrac{1}{32}\)
\(=1+1+1+1+1+1=6\) (đpcm)
#$\mathtt{Toru}$