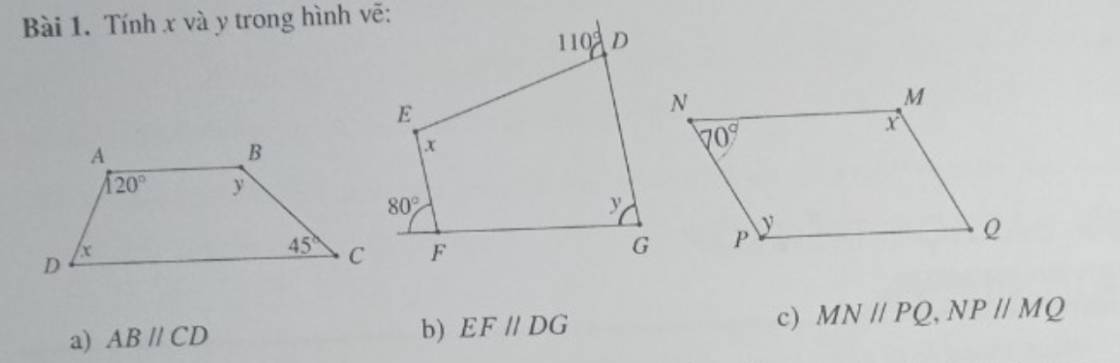
a: AB//CD
=>\(\widehat{A}+\widehat{D}=180^0\)
=>\(x+120^0=180^0\)
=>\(x=60^0\)
AB//CD
=>\(\widehat{B}+\widehat{C}=180^0\)
=>\(y+45^0=180^0\)
=>\(y=135^0\)
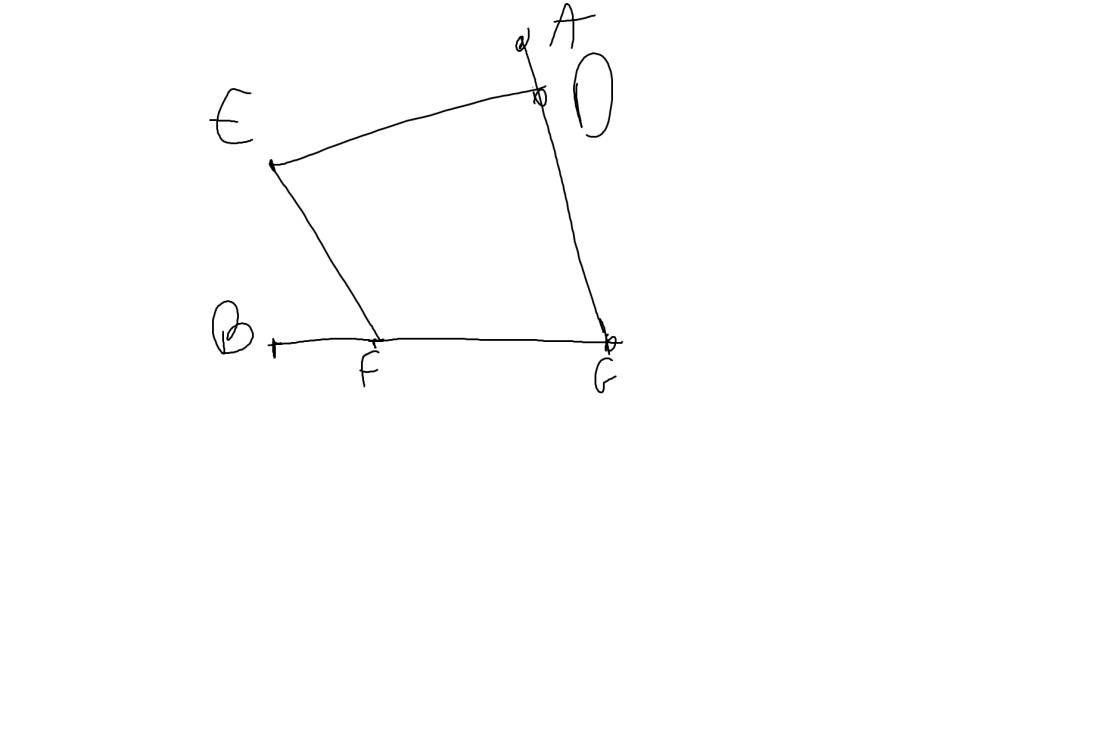
b: EF//DG
=>\(\widehat{EFB}=\widehat{DGF}\)(hai góc đồng vị)
=>\(y=80^0\)
Ta có: EF//DG
=>\(\widehat{FED}=\widehat{EDA}\)(hai góc so le trong)
=>\(x=110^0\)
c: Xét tứ giác MNPQ có
MN//PQ
MQ//NP
Do đó: MNPQ là hình bình hành
=>\(\widehat{M}=\widehat{P}=180^0-\widehat{N}=110^0\)
=>\(x=y=110^0\)
`\text{#nnguyen}`
`a)`
Ta có: `\text{AB // CD}`
`=>`\(\widehat{\text{DAB}}+\widehat{\text{ADC}}=180^0\Rightarrow x=180^0-\widehat{\text{DAB}}=180^0-120^0=60^0\)
Xét tứ giác `ABCD:`
$\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = 360^0$
$\Rightarrow y = 360^0 - (120^0 + 45^0 + 60^0) = 135^0$
`b)`
Vì `\text{EF // DG}`
`=>`$ \widehat{F} = \widehat{FGD} (\text{2 góc ở vị trí đồng vị})$
`=> y = 80^0`
Ta có: \(\widehat{\text{D}}+\widehat{\text{EDG}}=180^0\left(\text{kề bù}\right)\Rightarrow\widehat{\text{EDG}}=180^0-110^0=70^0\)
Tương tự, góc EFG = `180^0 - 80^0 = 100^0`
Xét tứ giác `EDGF:`
\(\widehat{\text{ }E}+\widehat{\text{EDG}}+\widehat{\text{FGD}}+\widehat{\text{EFG}}=360^0\)
`=> x = 360^0 - (70^0 + 80^0 + 100^0) = 110^0`
`c)`
Ta có: `\text{MN // PQ; NP // MQ}`
`=>` Tứ giác `MNPQ` là hình bình hành (định nghĩa)
Ta có: \(\widehat{\text{N}}+\widehat{\text{P}}=180^0\Rightarrow y=180^0-70^0=110^0\)
Hình bình hành có các góc đối bằng nhau
`=> x = y = 110^0.`