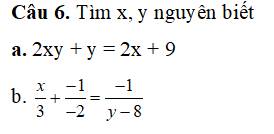a: 2xy+y=2x+9
=>2xy-2x+y-9=0
=>2x(y-1)+y-1=8
=>(y-1)(2x+1)=8
mà 2x+1 lẻ
nên \(\left(2x+1\right)\left(y-1\right)=1\cdot8=\left(-1\right)\cdot\left(-8\right)\)
=>\(\left(2x+1;y-1\right)\in\left\{\left(1;8\right);\left(-1;-8\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(0;9\right);\left(-1;-7\right)\right\}\)
b: \(\dfrac{x}{3}+\dfrac{-1}{-2}=\dfrac{-1}{y-8}\)
=>\(\dfrac{x}{3}+\dfrac{1}{2}=\dfrac{-1}{y-8}\)
=>\(\dfrac{2x+3}{6}=\dfrac{-1}{y-8}\)
=>(2x+3)(y-8)=-6
mà 2x+3 lẻ
nên \(\left(2x+3;y-8\right)\in\left\{\left(1;-6\right);\left(-1;6\right);\left(3;-2\right);\left(-3;2\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(-1;2\right);\left(-2;14\right);\left(0;6\right);\left(-3;10\right)\right\}\)