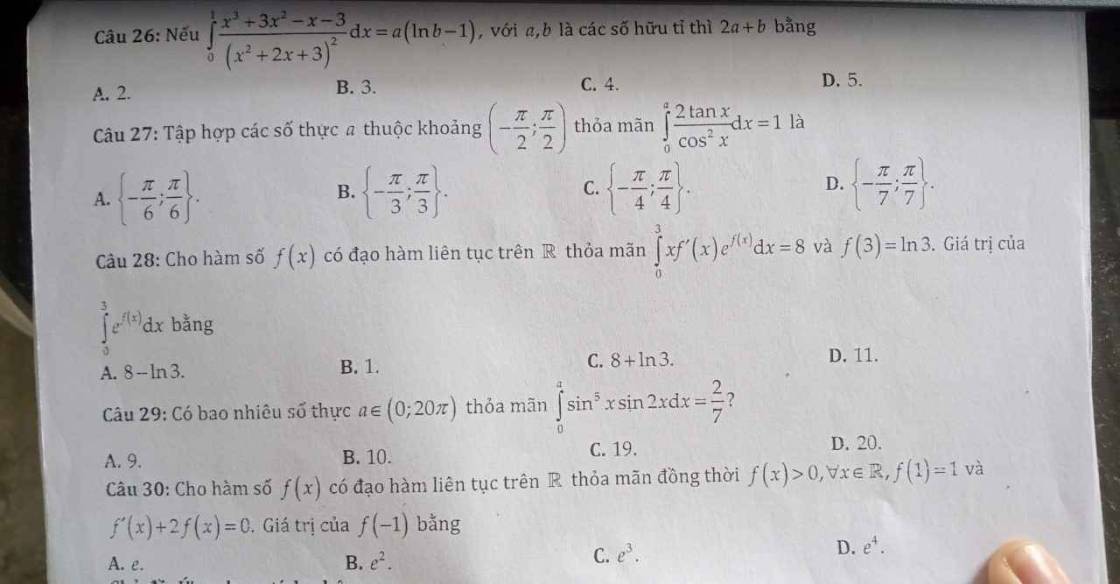26.
Do \(\dfrac{x^3+3x^2-x-3}{\left(x^2+2x+3\right)^2}=\dfrac{\left(x+1\right)\left(x^2+2x+3\right)-6\left(x+1\right)}{\left(x^2+2x+3\right)^2}\)
\(=\dfrac{x+1}{x^2+2x+3}-\dfrac{3\left(2x+2\right)}{\left(x^2+2x+3\right)^2}\)
\(\Rightarrow I=\int\limits^1_0\dfrac{-3d\left(x^2+2x+3\right)}{\left(x^2+2x+3\right)^2}+\dfrac{1}{2}\int\limits^1_0\dfrac{d\left(x^2+2x+3\right)}{x^2+2x+3}\)
\(=\dfrac{3}{x^2+2x+3}|^1_0+\dfrac{1}{2}ln\left(x^2+2x+3\right)|^1_0\)
\(=-\dfrac{1}{2}+\dfrac{1}{2}ln2=\dfrac{1}{2}\left(ln2-1\right)\)
\(\Rightarrow2a+b=1+2=3\)
27.
\(\int\dfrac{2tanx}{cos^2x}dx=\int2tanx.d\left(tanx\right)=tan^2x\)
\(\Rightarrow tan^2x|^a_0=1\Rightarrow tan^2a-tan^20=1\)
\(\Rightarrow tan^2a=1\Rightarrow a=\pm\dfrac{\pi}{4}\)
28.
Xét \(I=\int\limits^3_0x.f'\left(x\right).e^{f\left(x\right)}dx\)
Đặt \(\left\{{}\begin{matrix}u=x\\dv=f'\left(x\right).e^{f\left(x\right)}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^{f\left(x\right)}\end{matrix}\right.\)
\(\Rightarrow I=8=x.e^{f\left(x\right)}|^3_0-\int\limits^3_0e^{f\left(x\right)}dx\)
\(=3.e^{f\left(3\right)}-\int\limits^3_0e^{f\left(x\right)}dx\)
\(=9-\int\limits^3_0e^{f\left(x\right)}dx\)
\(\Rightarrow\int\limits^3_0e^{f\left(x\right)}dx=9-8=1\)
29.
\(f'\left(x\right)+2f\left(x\right)=0\)
\(\Leftrightarrow f'\left(x\right)=-2f\left(x\right)\)
\(\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=-2\)
Lấy nguyên hàm 2 vế:
\(\Rightarrow ln\left[f\left(x\right)\right]=\int-2dx=-2x+C\)
Thay \(x=1\)
\(\Rightarrow ln\left[f\left(1\right)\right]=-2.1+C\Rightarrow C=2\)
\(\Rightarrow ln\left[f\left(x\right)\right]=-2x+2\)
\(\Rightarrow f\left(x\right)=e^{-2x+2}\)
\(\Rightarrow f\left(-1\right)=e^4\)