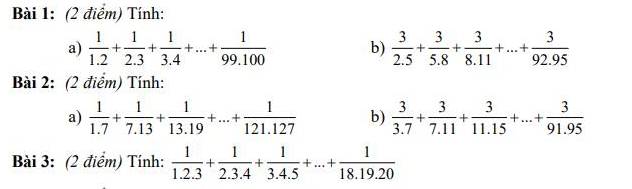Bài 1:
a: \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\)
b: \(\dfrac{3}{2\cdot5}+\dfrac{3}{5\cdot8}+...+\dfrac{3}{92\cdot95}\)
\(=\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{92}-\dfrac{1}{95}\)
\(=\dfrac{1}{2}-\dfrac{1}{95}=\dfrac{93}{190}\)
Bài 2:
a: \(\dfrac{1}{1\cdot7}+\dfrac{1}{7\cdot13}+...+\dfrac{1}{121\cdot127}\)
\(=\dfrac{1}{6}\left(\dfrac{6}{1\cdot7}+\dfrac{6}{7\cdot13}+...+\dfrac{6}{121\cdot127}\right)\)
\(=\dfrac{1}{6}\left(1-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{13}+...+\dfrac{1}{121}-\dfrac{1}{127}\right)\)
\(=\dfrac{1}{6}\left(1-\dfrac{1}{127}\right)=\dfrac{1}{6}\cdot\dfrac{126}{127}=\dfrac{21}{127}\)
b: \(\dfrac{3}{3\cdot7}+\dfrac{3}{7\cdot11}+...+\dfrac{3}{91\cdot95}\)
\(=\dfrac{3}{4}\left(\dfrac{4}{3\cdot7}+\dfrac{4}{7\cdot11}+...+\dfrac{4}{91\cdot95}\right)\)
\(=\dfrac{3}{4}\left(\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{91}-\dfrac{1}{95}\right)\)
\(=\dfrac{3}{4}\left(\dfrac{1}{3}-\dfrac{1}{95}\right)=\dfrac{3}{4}\cdot\dfrac{92}{3\cdot95}=\dfrac{23}{95}\)