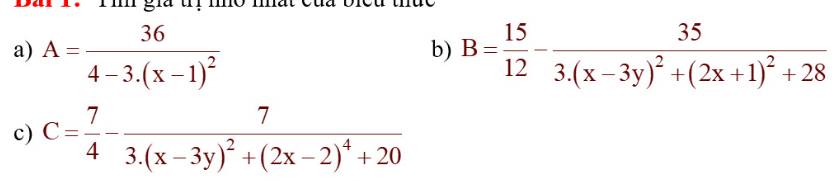a.
Do \(3\left(x-1\right)^2\ge0;\forall x\Rightarrow4-3\left(x-1\right)^2\le4;\forall x\)
Mà \(36>0\Rightarrow\dfrac{36}{4-3\left(x-1\right)^2}\ge\dfrac{36}{4}=9\)
Vậy \(A_{min}=9\) khi \(\left(x-1\right)^2=0\Rightarrow x=1\)
b.
Do \(\left\{{}\begin{matrix}3\left(x-3y\right)^2\ge0\\\left(2x+1\right)^2\ge0\end{matrix}\right.\) ; \(\forall x;y\)
\(\Rightarrow3\left(x-3y\right)^2+\left(2x+1\right)^2+28\ge28\) ; \(\forall x;y\)
Mà \(35>0\Rightarrow\dfrac{35}{3\left(x-3y\right)^2+\left(2x+1\right)^2+29}\le\dfrac{35}{28}\)
\(\Rightarrow\dfrac{15}{12}-\dfrac{35}{3\left(x-3y\right)^2+\left(2x+1\right)^2+28}\ge\dfrac{15}{12}-\dfrac{35}{28}=0\)
\(B_{min}=0\) khi \(\left\{{}\begin{matrix}x-3y=0\\2x+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{1}{6}\end{matrix}\right.\)
c.
Làm giống hệt câu b