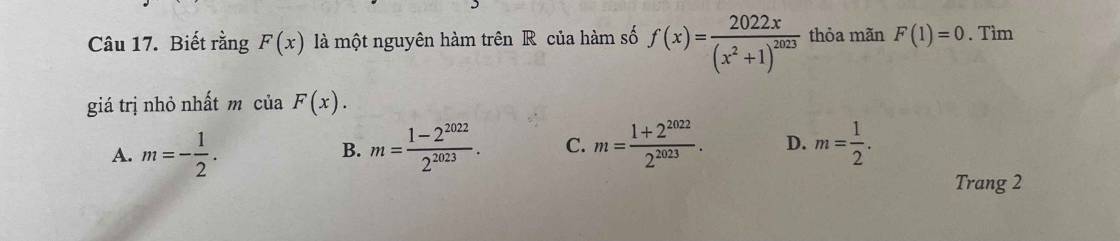Question

Answer 1

\(F\left(x\right)=\int\dfrac{2022x}{\left(x^2+1\right)^{2023}}dx=1011\int\dfrac{d\left(x^2+1\right)}{\left(x^2+1\right)^{2023}}=-\dfrac{1}{2}.\dfrac{1}{\left(x^2+1\right)^{2022}}+C\)

\(F\left(1\right)=0\Rightarrow C=\dfrac{1}{2.2^{2022}}=\dfrac{1}{2^{2023}}\)

\(\Rightarrow F\left(x\right)=-\dfrac{1}{2}.\dfrac{1}{\left(x^2+1\right)^{2022}}+\dfrac{1}{2^{2023}}\ge-\dfrac{1}{2}+\dfrac{1}{2^{2023}}=\dfrac{1-2^{2022}}{2^{2023}}\)