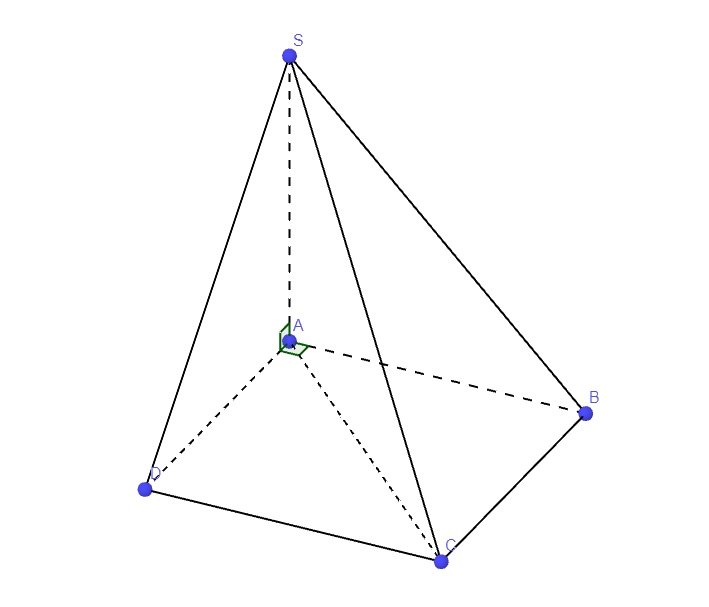
a: BC\(\perp\)AB(ABCD là hình vuông)
BC\(\perp\)SA(SA\(\perp\)(ABCD))
SA,AB cùng thuộc mp(SAB)
Do đó: BC\(\perp\)(SAB)
b: ta có: CD\(\perp\)AD(ABCD là hình vuông)
CD\(\perp\)SA(SA\(\perp\)(ABCD))
SA,AD cùng thuộc mp(SAD)
Do đó: CD\(\perp\)(SAD)
c: Ta có: BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
d: \(\widehat{SB;\left(ABCD\right)}=\widehat{BS;BA}=\widehat{SBA}\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\sqrt{2}\)
nên \(\widehat{SBA}\simeq54^044'\)
=>\(\widehat{SB;\left(ABCD\right)}\simeq54^044'\)
e: \(\widehat{SC;\left(ABCD\right)}=\widehat{CS;CA}=\widehat{SCA}\)
Vì ABCD là hình vuông
nên \(AC=AB\cdot\sqrt{2}=a\sqrt{2}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=1\)
nên \(\widehat{SCA}=45^0\)
=>\(\widehat{SC;\left(ABCD\right)}=45^0\)
f: Ta có: BA\(\perp\)AD(ABCD là hình vuông)
BA\(\perp\)SA(SA\(\perp\)(ABCD))
AD,SA cùng thuộc mp(SAD)
Do đó: BA\(\perp\)(SAD)
=>\(\widehat{SA;\left(SAD\right)}=\widehat{SA;SB}=\widehat{ASB}\)
Xét ΔSAB vuông tại A có \(tanASB=\dfrac{AB}{SA}=\dfrac{1}{\sqrt{2}}\)
nên \(\widehat{ASB}\simeq35^016'\)
=>\(\widehat{SA;\left(SAD\right)}\simeq35^016'\)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\\BC\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp BC\)
Lại có: \(AB\perp BC\) (ABCD là hình vuông)
\(\Rightarrow BC\perp\left(SAB\right)\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\\CD\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp CD\)
Lại có \(AD\perp CD\) (ABCD là hình vuông)
\(\Rightarrow CD\perp\left(SAD\right)\)
c.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\\BD\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp BD\)
Mà \(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow BD\perp\left(SAC\right)\)
d.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{2}\Rightarrow\widehat{SBA}\approx54^044'\)
e.
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
f.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\\AB\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp AB\)
Mà \(AB\perp AD\) (ABCD là hình vuông)
\(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow SA\) là hình chiếu vuông góc của SB lên (SAD)
\(\Rightarrow\widehat{ASB}\) là góc giữa SB và (SAD)
\(tan\widehat{ASB}=\dfrac{AB}{SA}=\dfrac{1}{\sqrt{2}}\Rightarrow\widehat{ASB}\approx35^016'\)