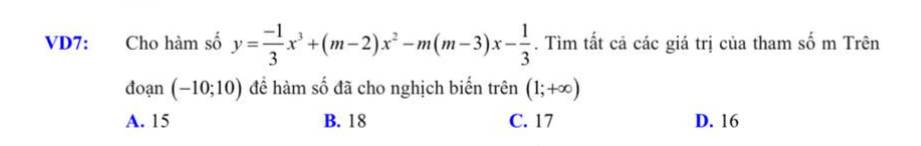\(y'=f\left(x\right)=-x^2+2\left(m-2\right)x-m\left(m-3\right)\)
\(\Delta'=\left(m-2\right)^2-m\left(m-3\right)=-m+4\)
TH1: \(-m+4\le0\Rightarrow m\ge4\) hàm nghịch biến trên R (thỏa mãn)
TH2: \(m< 4\)
Hàm nghịch biến trên khoảng đã cho khi \(x_1< x_2\le1\)
\(\Rightarrow\dfrac{2-m-\sqrt{4-m}}{-1}\le1\)
\(\Leftrightarrow2-m-\sqrt{4-m}+1\ge0\)
\(\Leftrightarrow4-m-\sqrt{4-m}-1\ge0\)
\(\Rightarrow\sqrt{4-m}\ge\dfrac{1+\sqrt{5}}{2}\)
\(\Rightarrow m\le\dfrac{5-\sqrt{5}}{2}\approx1,4\)
Vậy có: \(\left(9-4+1\right)+\left(1+9+1\right)=17\) giá trị m nguyên thỏa mãn
Đúng 2
Bình luận (0)
