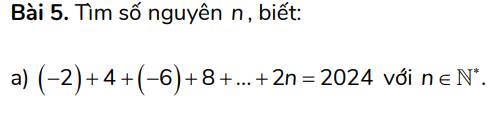\(\left(-2\right)+4+\left(-6\right)+8+...+2n=2024\)
=>\(\left(-1\right)+2+\left(-3\right)+4+...+n=1012\)
TH1: n chia hết cho 2
=>Dãy số -1;2;-3;4;..;n sẽ có n số hạng, n chẵn
=>Dãy số sẽ có n/2 cặp (-1;2);(-3;4);...(-n-1;n) có tổng là 1
(-1)+2+(-3)+4+...+n=1012
=>(-1+2)+(-3+4)+...+(-n+1)+n=1012
=>1+1+...+1=1012
=>n=1012
TH2: n lẻ
=>Dãy số (-1);2;(-3);4;...;n sẽ có n số hạng, n lẻ
=>Dãy số sẽ có \(\dfrac{n-1}{2}\) cặp số có tổng là 1 và một số lẻ ra là n
n lẻ nên n=2k+1
=>\(\dfrac{n-1}{2}=\dfrac{2k+1-1}{2}=\dfrac{2k}{2}=k\)
=>Phương trình sẽ trở thành:
(-1)+2+(-3)+4+...+...+(2k+1)=1012
=>(-1+2)+(-3+4)+...+(2k+3)+(-2k-2)+(2k+1)=1012
=>(-1+2)+(-3+4)+...+(2k+3-2k-2)+(2k+1)=1012
=>(2k+1)+1+...+1=1012
=>(2k+1)+k=1012
=>3k=1011
=>k=337
=>n=2*k+1=675
vậy: \(n\in\left\{1012;675\right\}\)