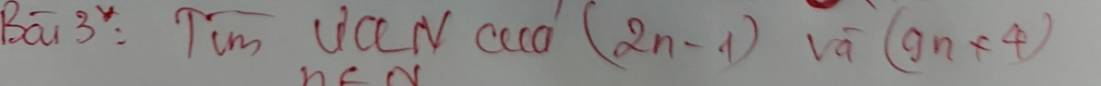Question

Answer 1

Lời giải:
Gọi $d=ƯCLN(2n-1, 9n+4)$

$\Rightarrow 2n-1\vdots d; 9n+4\vdots d$

$\Rightarrow 2(9n+4)-9(2n-1)\vdots d$

$\Rightarrow 17\vdots d\Rightarrow d\in\left\{1; 17\right\}$

Nếu $d=17$ thì $2n-1\vdots 17\Leftrightarrow 2n=17k+1$ với $k\in\mathbb{N}$

Do $2n$ chẵn nên $k$ lẻ. Đặt $k=2m+1$ với $m$ tự nhiên.

$2n=17(2m+1)+1=34m+18$

$\Rightarrow n=17m+9$

Vậy ƯCLN(2n-1, 9n+4)=17 nếu $n$ có dạng $17m+9$ với $m$ tự nhiên.

ƯCLN(2n-1, 9n+4)=1 với các TH $n$ còn lại.