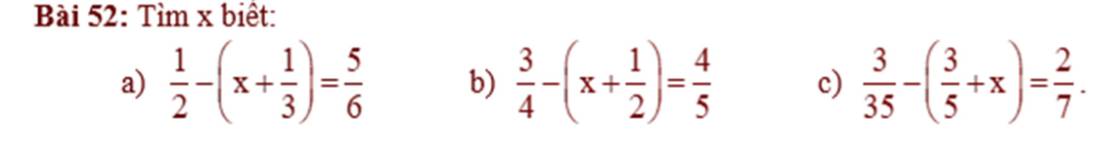\(a)\dfrac{1}{2}-\left(x+\dfrac{1}{3}\right)=\dfrac{5}{6}\\ x+\dfrac{1}{3}=\dfrac{1}{2}-\dfrac{5}{6}\\ x+\dfrac{1}{3}=-\dfrac{1}{3}\\ x=-\dfrac{1}{3}-\dfrac{1}{3}\\ x=-\dfrac{2}{3}\)
\(b)\dfrac{3}{4}-\left(x+\dfrac{1}{2}\right)=\dfrac{4}{5}\\ x+\dfrac{1}{2}=\dfrac{3}{4}-\dfrac{4}{5}\\ x+\dfrac{1}{2}=-\dfrac{1}{20}\\ x=-\dfrac{1}{20}-\dfrac{1}{2}\\ x=-\dfrac{11}{20}\)
\(c)\dfrac{3}{35}-\left(\dfrac{3}{5}+x\right)=\dfrac{2}{7}\\ \dfrac{3}{5}+x=\dfrac{3}{35}-\dfrac{2}{7}\\ \dfrac{3}{5}+x=-\dfrac{1}{5}\\ x=-\dfrac{1}{5}-\dfrac{3}{5}\\ x=-\dfrac{4}{5}.\)
\(a>\) \(\dfrac{1}{2}-\left(x+\dfrac{1}{3}\right)=\dfrac{5}{6}\)
\(x+\dfrac{1}{3}=\dfrac{1}{2}-\dfrac{5}{6}\)
\(x+\dfrac{1}{3}=-\dfrac{1}{3}\)
\(x=-\dfrac{1}{3}-\dfrac{1}{3}\)
\(x=-\dfrac{2}{3}\)
\(b>\) \(\dfrac{3}{4}-\left(x+\dfrac{1}{2}\right)=\dfrac{4}{5}\)
\(x+\dfrac{1}{2}=\dfrac{3}{4}-\dfrac{4}{5}\)
\(x+\dfrac{1}{2}=-\dfrac{1}{20}\)
\(x=-\dfrac{1}{20}-\dfrac{1}{2}\)
\(x=-\dfrac{11}{20}\)
\(c>\) \(\dfrac{3}{35}-\left(\dfrac{3}{5}+x\right)=\dfrac{2}{7}\)
\(\dfrac{3}{5}+x=\dfrac{3}{35}-\dfrac{2}{7}\)
\(\dfrac{3}{5}+x=-\dfrac{1}{5}\)
\(x=-\dfrac{1}{5}-\dfrac{3}{5}\)
\(x=-\dfrac{4}{5}\)
\(a,\dfrac{1}{2}-\left(x+\dfrac{1}{3}\right)=\dfrac{5}{6}\)
\(x+\dfrac{1}{3}=\dfrac{1}{2}-\dfrac{5}{6}\)
\(x+\dfrac{1}{3}=-\dfrac{1}{3}\)
\(x=-\dfrac{1}{3}-\dfrac{1}{3}\)
\(x=-\dfrac{2}{3}\)
\(---\)
\(b,\dfrac{3}{4}-\left(x+\dfrac{1}{2}\right)=\dfrac{4}{5}\)
\(x+\dfrac{1}{2}=\dfrac{3}{4}-\dfrac{4}{5}\)
\(x+\dfrac{1}{2}=-\dfrac{1}{20}\)
\(x=-\dfrac{1}{20}-\dfrac{1}{2}\)
\(x=-\dfrac{11}{20}\)
\(---\)
\(c,\dfrac{3}{35}-\left(\dfrac{3}{5}+x\right)=\dfrac{2}{7}\)
\(\dfrac{3}{5}+x=\dfrac{3}{35}-\dfrac{2}{7}\)
\(\dfrac{3}{5}+x=-\dfrac{1}{5}\)
\(x=-\dfrac{1}{5}-\dfrac{3}{5}\)
\(x=-\dfrac{4}{5}\)
#\(Toru\)